湖北省黄石市下陆区2018-2019学年七年级上学期数学期中考试试卷

试卷更新日期：2018-11-13 类型：期中考试

进入出卷网下载

一、单选题

1. a的相反数是（）

A、|a| B、 $\frac{1}{a}$ C、－a D、以上都不对

查看试题解析
2. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入100元记作+100元．那么﹣80元表示（）

A、支出20元 B、收入20元 C、支出80元 D、收入80元

查看试题解析
3. 在1，－2，0，53这四个数中，最大的数是（）

A、－2 B、0 C、53 D、1

查看试题解析
4. 若数轴上表示﹣2和3的两点分别是点A和B，则点A和点B之间的距离是（）

A、﹣5 B、﹣1 C、1 D、5

查看试题解析
5. 长方形窗户上的装饰物如图所示，它是由半径均为b的两个四分之一圆组成，则能射进阳光部分的面积是（）

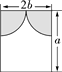A、2a²－πb² B、2a²－ $\frac{π}{2}$ b² C、2ab－πb² D、2ab－ $\frac{π}{2}$ b²

查看试题解析
6. 如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作；然后，将其中的一个小三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个小三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；……，根据以上操作，若要得到100个小三角形，则需要操作的次数是（）

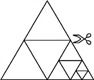A、25 B、33 C、34 D、50

查看试题解析
7. 一次数学达标检测的成绩以80分为标准成绩，“奋斗”小组4名学生的成绩与标准成绩的差如下：－7分、－6分、+9分、+2分，他们的平均成绩为（）

A、78分 B、82分 C、80.5分 D、79.5分

查看试题解析
8. 计算－3＋(－1)的结果是（）

A、2 B、－2 C、4 D、－4

查看试题解析
9. 等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和－1，若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2012次后，点B（）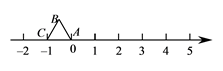

A、不对应任何数 B、对应的数是2010 C、对应的数是2011 D、对应的数是2012

查看试题解析
10. 已知a，b，c为非零的实数，则 $\frac{a}{| a |} + \frac{a b}{| a b |} + \frac{a c}{| a c |} + \frac{b c}{| b c |}$ 的可能值的个数为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 某地某天的最高气温是6℃，最低气温是﹣4℃，则该地当天的温差为℃．

查看试题解析
12. 若a－3=0，则a的相反数是．

查看试题解析
13. 点A表示数轴上的一个点，将点A向右移动7个单位，再向左移动4个单位，终点恰好是原点，则点A表示的数是.

查看试题解析
14. 规定图形表示运算a-b+c，图形表示运算x+z-y-w，则 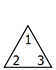+ =（直接写出答案）.

查看试题解析
15. 已知|x|＝2，|y|＝5，且x＞y，则x＋y＝．

查看试题解析
16. 已知两个完全相同的大长方形，长为a，各放入四个完全一样的白色小长方形后，得到图①、图②，那么，图①中阴影部分的周长与图②中阴影部分的周长的差是(用含a的代数式表示)．

查看试题解析

三、解答题

17. 计算题：

(1)、(－78) +(+5)+(+78)

(2)、(+23)+(－17)+(+6)+(－22)

(3)、[45－( $\frac{7}{9}$ － $\frac{11}{12}$ + $\frac{5}{6}$ )×36]÷5

(4)、99 $\frac{71}{72}$ ×(－36)

查看试题解析
18. 先化简，再求值：－a²b＋(3ab²－a²b)－2(2ab²－a²b)，其中 a＝－1，b＝－2.

查看试题解析
19. 若多项式4xⁿ⁺²﹣5x²^﹣ⁿ+6是关于x的三次多项式，求代数式n³﹣2n+3的值．

查看试题解析
20. 某自行车厂一周计划生产1050辆自行车，平均每天生产150辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）：

(1)、根据记录可知前三天共生产辆；

(2)、产量最多的一天比产量最少的一天多生产辆；

(3)、该厂实行计件工资制，每辆车50元，超额完成任务每辆奖10元，少生产一辆扣10元，那么该厂工人这一周的工资总额是多少？

查看试题解析
21. 操作探究：已知在纸面上有一数轴(如图所示)．

(1)、操作一：
折叠纸面，使1表示的点与－1表示的点重合，则－3表示的点与表示的点重合；

(2)、操作二：
折叠纸面，使－1表示的点与3表示的点重合，回答以下问题：
①5表示的点与数表示的点重合；
②若数轴上A、B两点之间距离为11(A在B的左侧)，且A、B两点经折叠后重合，求A、B两点表示的数是多少．

查看试题解析
22. 如图，老王开车从A到D，全程共72千米．其中AB段为平地，车速是30千米/小时，BC段为上山路，车速是22.5千米/小时，CD段为下山路，车速是36千米/小时，已知下山路是上山路的2倍．

(1)、若AB=6千米，老王开车从A到D共需多少时间？

(2)、当BC的长度在一定范围内变化时，老王开车从A到D所需时间是否会改变？为什么？（给出计算过程）

查看试题解析
23. 探索规律，观察下面算式，解答问题．
1＋3＝4＝2²；
1＋3＋5＝9＝3²；
1＋3＋5＋7＝16＝4²；
1＋3＋5＋7＋9＝25＝5²；
…

(1)、请猜想：1＋3＋5＋7＋9＋…＋19＝；

(2)、请猜想：1＋3＋5＋7＋9＋…＋(2n－1)＋(2n＋1)＋(2n＋3)＝；

(3)、试计算：101＋103＋…＋197＋199.

查看试题解析