新人教版数学七年级下册 第五章相交线与平行线5.2.1平行线同步练习
试卷更新日期：2015-08-27 类型：同步测试
一、基础练习
-
1. 根据下列要求画图．
(1)、如图(1)所示，过点A画MN∥BC；(2)、如图(2)所示，过点P画PE∥OA，交OB于点E，过点P画PH∥OB，交OA于点H；(3)、如图(3)所示，过点C画CE∥DA，与AB交于点E，过点C画CF∥DB，与AB的延长线交于点F． -
2. 在同一平面内，两条不重合直线的位置关系可能是( )A、平行或相交 B、垂直或相交 C、垂直或平行 D、平行、垂直或相交
-
3. 在同一平面内有三条直线，若其中有两条且只有两条直线平行，则它们交点的个数为( )A、0 个 B、1个 C、2个 D、3个
-
4. 下列说法正确的有( )
①不相交的两条直线是平行线；②在同一平面内，两条直线的位置关系有两种；
③若线段AB与CD没有交点，则AB∥CD；④若a∥b，b∥c，则a与c不相交．
A、1个 B、2个 C、3个 D、4个 -
5. 过一点画已知直线的平行线，则( )A、有且只有一条 B、有两条 C、不存在 D、不存在或只有一条
-
6. 在同一平面内，叫做平行线．
-
7. 若AB∥CD，AB∥EF，则∥ ， 理由是 ．
-
8. 在同一平面内，若两条直线相交，则公共点的个数是；若两条直线平行，则公共点的个数是 ．
-
9. 同一平面内的三条直线，其交点的个数可能为 ．
-
10. 直线L同侧有A，B，C三点，若过A，B的直线L1和过B，C的直线L2都与L平行，则A，B，C三点 ， 理论根据是 ．
-
11. 已知直线a∥b，b∥c，c∥d，则a与d的关系是什么？为什么？
-
12. 如图所示，梯形ABCD中，AD∥BC，P是AB的中点，过P点作AD的平行线交DC于Q点．
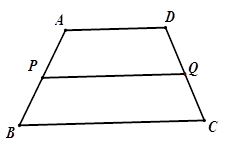(1)、PQ与BC平行吗？为什么？(2)、测DQ与CQ的长，DQ与CQ是否相等？ -
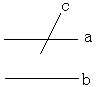
13. 如图所示，a∥b，a与c相交，那么b与c相交吗？为什么？
-
14. 下列说法正确的是( )A、经过一点有一条直线与已知直线平行 B、经过一点有无数条直线与已知直线平行 C、经过一点有且只有一条直线与已知直线平行 D、经过直线外一点有且只有一条直线与已知直线平行
-
15. 平面内两条的直线叫平行线，如果直线a与直线b平行可记为 ， 读作 ．
-
16. 过直线外一点 与已知直线平行。
-
17. 如果两条直线和第三条直线 ， 那么这两条直线平行；若a∥b ， b∥c，则 ．
-
18. 在同一平面内，不互相重合的两条直线位置关系有种，它们是 ， ．
-
19. 在同一平面内L1与L2没有公共点，则L1L2 ．
-
20. 在同一平面内L1和L2有一个公共点，则L1与L2 ．
-
21. 在同一平面内，不重合的两条直线的位置关系有种，分别是 ， ．
-
22. 设a，b，c为平面内三条不同直线：
①若a∥b，c⊥a，则b与c的位置关系是；
②若a∥b，b∥c，则a与c的位置关系是 ．
-
23. 在同一平面内三条直线交点有多少个？
甲：同一平面三直线相交交点的个数为0个，因为a∥b∥c，如图（1）所示．
乙：同一平面内三条直线交点个数只有1个，因为a，b，c交于同一点O，如图（2）所示．
以上说法谁对谁错？为什么？
-
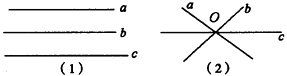
24. 请举出一例生活中平行线的例子，如笔直铁路上铁轨是互相平行的直线．
举例：
-
25. 公路两旁的两根电线杆位置关系是 ．
-
26. 练习本中的横线格中的横线段位置关系是 ， 如图所示．
-
27.
如图所示，AB∥CD，EF与AB，CD相交，EF与AB交于点 ， EF与CD交于点 ．
二、课堂检测
-
28. 下列说法不正确的是（ ）A、过马路的斑马线是平行线 B、100米跑道的跑道线是平行线 C、若a∥b，b∥d，则a⊥d D、过直线外一点有且只有一条直线与已知直线平行
-
29. 下列说法正确的是（ ）A、同一平面内不相交的两线段必平行 B、同一平面内不相交的两射线必平行 C、同一平面内不相交的一条线段与一条直线必平行 D、同一平面内不相交的两条直线必平行
-
30. 如图所示，在这些四边形AB不平行于CD的是（ ）A、
B、
C、
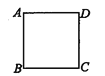D、
-
31. 如图所示，在∠AOB内有一点P．
①过P画L1∥OA；
②过P画L2∥OB；
③用量角器量一量L1与L2相交的角与∠O的大小有怎样关系？ -
32. （教材变式题）“垂直于同一条直线的两直线平行”，运用这一性质可以说明铺设铁轨互相平行的道理．
如图所示，已知∠2是直角，再度量出∠1或∠3就会知道铁轨平行不平行？
[解答]
方案一：若量得∠3=90°，结合∠2情况，说明理由．
方案二：若量得∠1=90°，结合∠2情况，说明理由．
-
33. （原创题）如图所示，在书写艺术字时，常常运用画“平行线段”这种基本作图方法，此图是在书写字“M”：
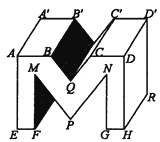(1)、请从正面，上面，右侧三个不同方向上各找出一组平行线段，并用字母表示出来；(2)、EF与A′B′有何位置关系？CC′与DH有何位置关系？
