浙教版七年级下册第3章 3.4乘法公式 同步练习

试卷更新日期：2017-03-20 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 下列乘法算式中，不能用平方差公式进行运算的是（  ）
    A、（m+n）（﹣m﹣n） B、（﹣m+n）（﹣m﹣n） C、（﹣m﹣n）（m﹣n） D、（m+n）（﹣m+n）

    查看试题解析

  • 2. 已知9x2﹣30x+m是一个完全平方式，则m的值等于（　　）


    A、5 B、10 C、20 D、25

    查看试题解析

  • 3. 如图，把边长为（a+2）的正方形纸片剪出一个边长为a的正方形之后，剩余部分又剪拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为2，则长方形的面积是（  ）

    A、2（2a+2） B、2a+4 C、4a+8 D、2（a+4）

    查看试题解析

  • 4. 如图，有甲、乙、丙三种地砖，其中甲、乙是正方形，边长分别为a、b，丙是长方形，长为a，宽为b（其中a＞b），如果要用它们拼成若干个边长为（3a+b）的正方形，那么应取甲、乙、丙三种地砖块数的比是（   ）

    A、无法确定 B、2：1：2 C、3：1：2 D、9：1：6

    查看试题解析

  • 5. 如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则矩形的面积为（   ）
    A、（2a2+5a）cm2 B、（6a+15）cm2 C、（6a+9）cm2 D、（3a+15）cm2

    查看试题解析

  • 6. 计算下列各式，其结果是4y2﹣1的是（   ）
    A、（2y﹣1）2 B、（2y+1）（2y﹣1）   C、（﹣2y+1）（﹣2y+1） D、（﹣2y﹣1）（2y+1）

    查看试题解析

  • 7. 已知：x﹣y=5，（x+y）2=49，则x2+y2的值等于（   ）
    A、37 B、27 C、25 D、44

    查看试题解析

  • 8. 设（2a+3b）2=（2a﹣3b）2+A，则A=（   ）
    A、6ab B、12ab C、0 D、24ab

    查看试题解析

  • 9. 下列计算中正确的是（   ）
    A、（x+y）（y﹣x）=x2﹣y2 B、（﹣3x﹣2y）2=9x2+12xy+4y2 C、（3x﹣2）2=9x2﹣4 D、（3x﹣y）（3x+y）=3x2﹣y2

    查看试题解析

  • 10. 若关于x的二次三项式x2﹣ax+36是一个完全平方式，那么a的值是（   ）
    A、12 B、±12 C、6 D、±6

    查看试题解析

  • 11. 若a2﹣b2= 23 ，a﹣b= 12 ，则a+b的值为（   ）
    A、﹣ 12 B、43 C、32 D、2

    查看试题解析

  • 12. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（   ）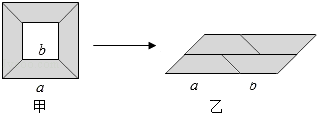

    A、a2﹣b2=（a﹣b）2 B、（a+b）2=a2+2ab+b2 C、（a﹣b）2=a2﹣2ab+b2 D、a2﹣b2=（a+b）（a﹣b）

    查看试题解析

二、填空题

  • 13. 若4x2+mx+25是一个完全平方式，则m的值是 ．

    查看试题解析

  • 14. 已知正方形的边长为a，如果它的边长增加3，那么它的面积增加了 ．

    查看试题解析

  • 15. 已知m＞0，如果x2+2（m﹣1）x+16是一个完全平方式，那么m的值为 ．

    查看试题解析

  • 16. 已知x+y=﹣5，xy=6，则x2+y2= ．

    查看试题解析

  • 17. 已知（x﹣a）（x+a）=x2﹣9，那么a= ．

    查看试题解析

  • 18. 如图，边长为（m+3）的正方形纸片剪出一个边长为m的正方形之后，剩余部分可剪拼成一个长方形（不重叠无缝隙），若拼成的长方形一边长为3，则这个长方形的周长是 ．

    查看试题解析

三、计算题

四、综合题

  • 21. 乘法公式的探究及应用．
    (1)、如图1，可以求出阴影部分的面积是（写成两数平方差的形式）；

    (2)、如图2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是 ， 长是 ， 面积是（写成多项式乘法的形式）；

    (3)、比较左、右两图的阴影部分面积，可以得到乘法公式（用式子表达）．

    查看试题解析

  • 22. 按要求完成下列各题：
    (1)、已知实数a、b满足（a+b）2=1，（a﹣b）2=9，求a2+b2﹣ab的值；
    (2)、已知（2015﹣a）（2016﹣a）=2047，试求（a﹣2015）2+（2016﹣a）2的值．

    查看试题解析

  • 23. 阅读下文，寻找规律：

    已知x≠1时，（1﹣x）（1+x）=1﹣x2 ， （1﹣x）（1+x+x2）=1﹣x3 ， （1﹣x）（1+x+x2+x3）=1﹣x4…

    (1)、（1﹣x）（）=1﹣x8

    (2)、观察上式，并猜想：①（1﹣x）（1+x+x2+…+xn）= ．

    ②（x﹣1）（x10+x9+…+x+1）= ．

    (3)、根据你的猜想，计算：

    ①（1﹣2）（1+2+22+23+24+25）= ．

    ②1+2+22+23+24+…+22007= ．

    查看试题解析

  • 24. 图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．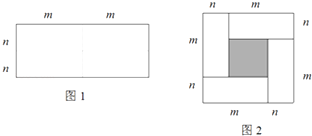

    (1)、请用两种不同的方法求图2中阴影部分的面积（直接用含m，n的代数式表示）

    方法1：

    方法2：

    (2)、根据（1）中结论，请你写出下列三个代数式之间的等量关系；代数式：（m+n）2 ， （m﹣n）2 ， mn
    (3)、根据（2）题中的等量关系，解决如下问题：已知a+b=8，ab=7，求a﹣b和a2﹣b2的值．

    查看试题解析

  • 25. 数学课上，我们知道可以用图形的面积来解释一些代数恒等式，如图1可以解释完全平方公式（a+b）2=a2+2ab+b2 ．

    (1)、如图2，请用不同的代数式表示图中阴影部分的面积，由此，你能得到怎样的等式？
    (2)、请说明这个等式成立；
    (3)、已知（2m+n）2=13，（2m﹣n）2=5，请利用上述等式求mn．

    查看试题解析