浙教版七年级下册第3章 3.3多项式的乘法 同步练习
试卷更新日期:2017-03-20 类型:同步测试
一、单选题
-
1. 如果(x+1)(x2﹣5ax+a)的乘积中不含x2项,则a为( )A、5 B、 C、- D、-52. 下列运算正确的是( )A、(a+b)2=a2+b2+2a B、(a﹣b)2=a2﹣b2 C、(x+3)(x+2)=x2+6 D、(m+n)(﹣m+n)=﹣m2+n23. 已知(x+a)(x+b)=x2﹣13x+36,则a+b=( )A、-5 B、5 C、-13 D、﹣13或54. 如果(x﹣2)(x+3)=x2+px+q,那么p、q的值为( )A、p=5,q=6 B、p=1,q=﹣6 C、p=1,q=6 D、p=5,q=﹣65. 若(x+3)(x+n)=x2+mx﹣21,则m的值为( )A、2 B、-2 C、4 D、-46. 要使(y2﹣ky+2y)(﹣y)的展开式中不含y2项,则k的值为( )A、﹣2 B、0 C、2 D、37. 已知(x+m)(x﹣n)=x2﹣3x﹣4,则m﹣n+mn的值为( )A、﹣1 B、7 C、1 D、﹣78. 如图,正方形卡片A类、B类和长方形卡片C类各若干张,如果要拼一个长为(a+3b),宽为(2a+b)的大长方形,则需要A类、B类和C类卡片的张数分别为( )
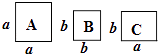 A、2,3,7 B、3,7,2 C、2,5,3 D、2,5,79. 通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )
A、2,3,7 B、3,7,2 C、2,5,3 D、2,5,79. 通过计算几何图形的面积可表示一些代数恒等式,如图可表示的代数恒等式是( )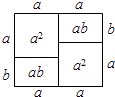 A、(a﹣b)2=a2﹣2ab+b2 B、(a+b)2=a2+2ab+b2 C、2a(a+b)=2a2+2ab D、(a+b)(a﹣b)=a2﹣b210. 李老师做了个长方形教具,其中一边长为2a+b,另一边长为a﹣b,则该长方形的面积为( )A、6a+b B、2a2﹣ab﹣b2 C、3a D、10a﹣b
A、(a﹣b)2=a2﹣2ab+b2 B、(a+b)2=a2+2ab+b2 C、2a(a+b)=2a2+2ab D、(a+b)(a﹣b)=a2﹣b210. 李老师做了个长方形教具,其中一边长为2a+b,另一边长为a﹣b,则该长方形的面积为( )A、6a+b B、2a2﹣ab﹣b2 C、3a D、10a﹣b二、填空题
-
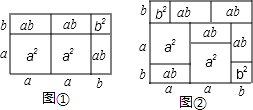
11. 若(x﹣1)(x+3)=ax2+bx+c,则a=、b=、c= .12. 若(1+x)(2x2+mx+5)的计算结果中x2项的系数为﹣3,则m=13. 如果要使(x+1)(x2﹣2ax+a2)的乘积中不含x2项,则a= .14. 已知x+y=5,xy=2,则(x+2)(y+2)= .15. 已知m﹣n=2,mn=﹣1,则(1+2m)(1﹣2n)的值为 .16. 若多项式5x2+2x﹣2与多项式ax+1的乘积中,不含x2项,则常数a= .17. 在我们所学的课本中,多项式与多项式相称可以用几何图形的面积来表示,例如:(2a+b)(a+b)=2a2+3ab+b2就可以用下面图中的图①来表示.请你根据此方法写出图②中图形的面积所表示的代数恒等式: .
三、计算题
-
18. 已知代数式(mx2+2mx﹣1)(xm+3nx+2)化简以后是一个四次多项式,并且不含二次项,请分别求出m,n的值,并求出一次项系数.19. 若(x2+3mx﹣)(x2﹣3x+n)的积中不含x和x3项,
(1)求m2﹣mn+n2的值;
(2)求代数式(﹣18m2n)2+(9mn)﹣2+(3m)2014n2016的值.
20. 对于任何实数,我们规定符号的意义是:=ad﹣bc.(1)按照这个规定请你计算:的值.
(2)按照这个规定请你计算:当x2﹣3x+1=0时,的值.
四、解答题
-
21. 若3x2﹣2x+b与x2+bx﹣1的和中不存在含x的项,试求b的值,写出它们的和,并证明不论x取什么值,它的值总是正数.22.
眉山市三苏雕像广场是为了纪念三苏父子而修建的.原是一块长为(4a+2b)米,宽为(3a﹣b)米的长方形地块,现在政府对广场进行改造,计划将如图四周阴影部分进行绿化,中间将保留边长为(a+b)米的正方形三苏父子雕像,则绿化的面积是多少平方米?并求出当a=20,b=10时的绿化面积.
 23.
23.如图①,在边长为3a+2b的大正方形纸片中,剪掉边长2a+b的小正方形,得到图②,把图②阴影部分剪下,按照图③拼成一个长方形纸片.

(1)求出拼成的长方形纸片的长和宽;
(2)把这个拼成的长方形纸片的面积加上10a+6b后,就和另一个长方形的面积相等.已知另一长方形的长为5a+3b,求它的宽.
24.当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2 .
 (1)、由图2,可得等式: .(2)、利用(1)中所得到的结论,解决下面的问题:
(1)、由图2,可得等式: .(2)、利用(1)中所得到的结论,解决下面的问题:已知 a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)、利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);(4)、小明用2 张边长为a 的正方形,3 张边长为b的正方形,5 张边长分别为a、b 的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为 .五、综合题
-
25.
乘法公式的探究及应用.
 (1)、如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);(2)、如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 面积是 (写成多项式乘法的形式);(3)、比较图1、图2阴影部分的面积,可以得到公式 ;(4)、运用你所得到的公式,计算下列各题:
(1)、如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);(2)、如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 面积是 (写成多项式乘法的形式);(3)、比较图1、图2阴影部分的面积,可以得到公式 ;(4)、运用你所得到的公式,计算下列各题:①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).