2018-2019学年数学北师大版九年级上册第四章图形的相似单元检测b卷

试卷更新日期：2018-11-09 类型：单元试卷

进入出卷网下载

一、选择题：

1. 如果 $\frac{b}{a} = \frac{3}{5}$ ，则 $\frac{a + b}{a} =$ （）

A、 $\frac{2}{3}$ B、 $\frac{8}{5}$ C、 $\frac{2}{5}$ D、 $\frac{8}{3}$

查看试题解析
2. 若 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4} \neq 0$ ，则 $\frac{2 a - b + c}{2 a} =$ （）

A、 $\frac{4}{5}$ B、 $\frac{5}{4}$ C、 $\frac{3}{4}$ D、无法确定

查看试题解析
3. 如图直线AB、CD、EF被直线a、b所截，若∠1=100°，∠2=100°，∠3=125°，∠4=55°，下列结论错误的是（）

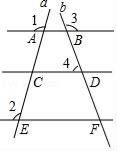A、EF∥CD∥AB B、 $\frac{A C}{C E} = \frac{B D}{D F}$ C、 $\frac{A B}{D C} = \frac{A C}{D F}$ D、 $\frac{A C}{A E} = \frac{B D}{B F}$

查看试题解析
4. 如图，在矩形ABCD中，E，F分别为，AD与BC的中点，且矩形ABCD相似矩形AEFB， $\frac{A D}{A B}$ 的值为（）

A、2 B、 $\frac{5}{3}$ C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
5. 如图，在△ABC中，D、E分别为AB、AC边上的点，DE // BC， $B E$ 与 $C D$ 相交于点F，则下列结论一定正确的是（）

A、 $\frac{D F}{F C} = \frac{A E}{A C}$ B、 $\frac{A D}{A B} = \frac{E C}{A C}$ C、 $\frac{A D}{A B} = \frac{D E}{B C}$ D、 $\frac{D F}{B F} = \frac{E F}{F C}$

查看试题解析
6. 以下条件不可以判定 $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 相似的是（）

A、 $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}} = \frac{B C}{B^{'} C^{'}}$ B、 $\frac{A B}{A^{'} B^{'}} = \frac{A C}{A^{'} C^{'}}$ ，且 $∠ A = ∠ A^{'}$ ’ C、 $∠ A = ∠ B^{'}$ ， $∠ B = ∠ C^{'}$ ’ D、 $\frac{A C}{A^{'} C^{'}} = \frac{B C}{B^{'} C^{'}}$ ，且 $∠ A = ∠ A^{'}$ ’

查看试题解析
7. 如图， $E F ∥ A C$ ， $G H ∥ A B$ ， $M N ∥ B C$ ， $E F$ 、 $G H$ 、 $M N$ 、交于点P，则图中与 $△ P G F$ 相似的三角形的个数是（）个．

A、4 B、5 C、6 D、7

查看试题解析
8. 如图，已知△ABC中，AD，AE，AF分别是三角形的高线，角平分线及中线，那么下列结论错误的是（）

A、AD⊥BC B、BF=CF C、BE=EC D、∠BAE=∠CAE

查看试题解析
9. 如图，在 $5 \times 5$ 的正方形方格中， $△ A B C$ 的顶点都在边长为1的小正方形的顶点上，作一个与 $△ A B C$ 相似的 $△ D E F$ ，使它的三个顶点都在小正方形的顶点上，则 $△ D E F$ 的最大面积是（）

A、5 B、10 C、 $\frac{5}{2}$ D、 $\sqrt{5}$

查看试题解析
10. 如图， $△ A B C \sim △ A^{'} B^{'} C^{'}$ ， $A D$ 、 $B E$ 分别是 $△ A B C$ 的高和中线， $A^{'} D^{'}$ 、 $B^{'} E^{'}$ 分别是 $△ A^{'} B^{'} C$ 的高和中线，且 $A D = 4$ ， $A^{'} D^{'} = 3$ ， $B E = 6$ ，则 $B^{'} E^{'}$ 的长为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{2}$ C、 $\frac{7}{2}$ D、 $\frac{9}{2}$

查看试题解析
11. 如图，四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形，若OA′：A′A=2：1，四边形A′B′C′D′的面积为12cm² ，则四边形 ABCD 的面积为（）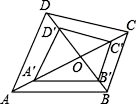

A、24cm² B、27cm² C、36cm² D、54cm²

查看试题解析
12. 如图，矩形ABCD的边长AD=3，AB=2，E为AB的中点，F在边BC上，且BF=2FC，AF分别与DE、DB相交于点M，N，则MN的长为（）

A、 $\frac{2 \sqrt{2}}{5}$ B、 $\frac{9 \sqrt{2}}{20}$ C、 $\frac{3 \sqrt{2}}{4}$ D、 $\frac{4 \sqrt{2}}{5}$

查看试题解析

二、填空题：

13. 如图，△ABC中，AD是中线，BC=8，∠B=∠DAC，则线段 $A C$ 的长为．

查看试题解析
14. 如图，在△ABC中，D，E分别为AB，AC上的点，若DE∥BC， $\frac{A D}{A B} = \frac{1}{3}$ ，则 $\frac{A D + D E + A E}{A B + B C + A C}$ =.

查看试题解析
15. 如图所示，阴影部分的面积是 $2 c m^{2}$ ，AE=ED， $B D = 2 C D$ ，则 $△ A B C$ 的面积是cm² ．

查看试题解析
16. 如图，已知CO₁是△ABC的中线，过点O₁作O₁E₁∥AC交BC于点E₁ ，连接AE₁交CO₁于点O₂；过点O₂作O₂E₂∥AC交BC于点E₂ ，连接AE₂交CO₁于点O₃；过点O₃作O₃E₃∥AC交BC于点E₃ ， …，如此继续，可以依次得到点O₄ ， O₅ ， …，O_n和点E₄ ， E₅ ， …，E_n ，则O₂₀₁₆E₂₀₁₆=AC．

查看试题解析

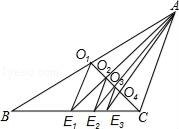
三、解答题.

17. 如图，在△ABC中，AM是BC边上的中线，直线DN∥AM，交AB于点D，交CA的延长线于点E，交BC于点N．求证： $\frac{A D}{A B} = \frac{A E}{A C}$ ．

查看试题解析
18. 如图，点E是四边形ABCD的对角线BD上一点，且∠BAC=∠BDC=∠DAE．求证：△ABE∽△ACD．

查看试题解析
19. 如图，是一个照相机成像的示意图，像高MN，景物高度AB、CD为水平视线，根据物体成像原理知：AB∥MN，CD⊥MN．

(1)、如果像高MN是35mm，焦距CL是50mm，拍摄的景物高度AB是4.9m，拍摄点离景物的距离LD是多少？

(2)、如果要完整的拍摄高度是2m的景物，拍摄点离景物有4m，像高不变，则相机的焦距应调整为多少毫米？

查看试题解析
20. 如图，△ABC三个顶点的坐标分别为A（－1，3），B（－1，1），C（－3，2）.

(1)、请画出△ABC关于y轴对称的△A₁B₁C₁；

(2)、以原点O为位似中心，将△A₁B₁C₁放大为原来的2倍，得到△A₂B₂C₂ ，求出△A₁B₁C₁与△A₂B₂C₂的面积.

查看试题解析
21. 如图，BE是△ABC的角平分线，延长BE至D，使得BC=CD．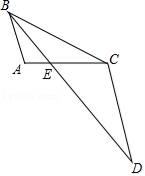

(1)、求证：△AEB∽△CED；

(2)、若AB=2，BC=4，AE=1，求CE长．

查看试题解析
22. 如图，在正方形ABCD中，点E，F分别是边AD，BC的中点，连接DF，过点E作EH⊥DF，垂足为H，EH的延长线交DC于点G．

(1)、猜想DG与CF的数量关系，并证明你的结论；

(2)、过点H作MN∥CD，分别交AD，BC于点M，N，若正方形ABCD的边长为10，点P是MN上一点，求△PDC周长的最小值．

查看试题解析
23. 如图，在平面直角坐标系中，直线y=﹣ $\frac{4}{3}$ x+ $\frac{40}{3}$ 与x轴、y轴分别交于点B、A，与直线y= $\frac{4}{3} x$ 相交于点C．动点P从O出发在x轴上以每秒5个单位长度的速度向B匀速运动，点Q从C出发在OC上以每秒4个单位长度的速度，向O匀速运动，运动时间为t秒（0＜t＜2）．

(1)、直接写出点C坐标及OC、BC长；

(2)、连接PQ，若△OPQ与△OBC相似，求t的值；

(3)、连接CP、BQ，若CP⊥BQ，直接写出点P坐标．

查看试题解析

2018-2019学年数学北师大版九年级上册第四章 图形的相似 单元检测b卷

一、选择题：

二、填空题：

三、解答题.

2018-2019学年数学北师大版九年级上册第四章图形的相似单元检测b卷