2018-2019学年数学北师大版九年级上册4.7 相似三角形的性质同步练习

试卷更新日期：2018-11-09 类型：同步测试

进入出卷网下载

1. 若△ABC∽△A`B`C`，则相似比k等于（）

A、A′B′：AB B、∠A： ∠A′ C、S_△ABC：S_△A′_B′_C′ D、△ABC周长：△A′B′C′周长

查看试题解析
2. 把一个三角形改成和它相似的三角形，如果面积扩大到原来的100倍，那么边长扩大到原来的（）

A、10000倍 B、10倍 C、100倍 D、1000倍

查看试题解析
3.
有一块直角边AB=3cm，BC=4cm的Rt△ABC的铁片，现要把它加工成一个正方形（加工中的损耗忽略不计），则正方形的边长为（　　）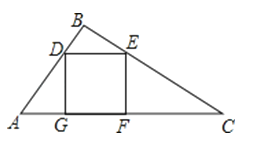

A、 $\frac{6}{7}$ B、 $\frac{30}{37}$ C、 $\frac{12}{7}$ D、 $\frac{60}{37}$

查看试题解析
4. 如图所示，两个等边三角形，两个矩形，两个正方形，两个菱形各成一组，每组中的一个图形在另一个图形的内部，对应边平行，且对应边之间的距离都相等，那么两个图形对应边不成比例的一组是（）

A、 B、 C、 D、

查看试题解析
5. 一张等腰三角形纸片，底边长15cm，底边上的高长22.5cm，现沿底边依次从下往上裁剪宽度均为3cm的矩形纸条，如图所示，已知剪得的纸条中有一张是正方形，则这张正方形纸条是（）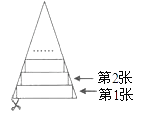

A、第4张 B、第5张 C、第6张 D、第7张

查看试题解析

6. 已知△ABC∽△DEF ，且它们的面积之比为4：9，则它们的相似比为．

查看试题解析
7. 顺次连接三角形三边上的中点所构成的三角形的高与原三角形对应高的比．

查看试题解析
8. 两个相似三角形面积之比为2：7，较大三角形一边上的高为 $\sqrt{2}$ ，则较小三角形的对应边上的高为.

查看试题解析
9. 两个相似三角形一组对应角平分线的长分别是2 cm和5 cm，那么这两个三角形的相似比是，如果在这两个三角形的一组对应中线中，较短的中线是3 cm，那么较长的中线是cm.

查看试题解析
10. 已知△ABC与△A₁B₁C₁的相似比为2：3，△A₁B₁C₁与△A₂B₂C₂的相似比为3：5，那么△ABC与△ A₂B₂C₂的相似比为。

查看试题解析

11. 如图，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知AB=4．

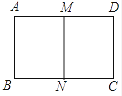(1)、求AD的长；

(2)、求矩形DMNC与矩形ABCD的相似比．

查看试题解析
12. 已知：如图，△ABC∽△ADE ， AE：EC=5：3，BC=6cm，∠A=40°，∠C=45°．

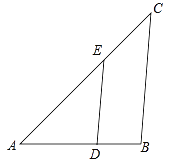(1)、求∠ADE的大小；

(2)、求DE的长．

查看试题解析
13. 有一块三角形铁片ABC，BC=12．高AH=8，按图(1)、(2)两种设计方案把它加工成一块矩形铁片DEFG，且要求矩形的长是宽的2倍，为了减少浪费，加工成的矩形铁片的面积应尽量大些．请你通过计算判断(1)、(2)两种设计方案哪个更好．

查看试题解析
14. 如图，光源L距地面（LN）8m，距正方体大箱顶站（LM）2m，已知，在光源照射下，箱子在左侧的影子BE长5m，求箱子在右侧的影子CF的长．（箱子边长为6m）

查看试题解析
15. △ABC∽△A`B`C`， $\frac{A B}{A^{'} B^{'}} = \frac{1}{2}$ ，边上的中线CD＝4cm，△ABC的周长为20cm，△A`B`C`的面积是64 cm² ，求：

(1)、A`B`边上的中线C`D`的长；

(2)、△A`B`C`的周长

(3)、△ABC的面积

查看试题解析

2018-2019学年数学北师大版九年级上册4.7 相似三角形的性质 同步练习