2018-2019学年数学北师大版九年级上册4.5 相似三角形判定定理的证明同步练习

试卷更新日期：2018-11-09 类型：同步测试

进入出卷网下载

1. 下列命题中是真命题的是（）

A、有一个角相等的直角三角形都相似 B、有一个角相等的等腰三角形都相似 C、有一个角是120°的等腰三角形都相似 D、两边成比例且有一角相等的三角形都相似

查看试题解析
2. 如图，在△ABC中，如果DE与BC不平行，那么下列条件中，不能判断△ADE∽△ACB的是（）

A、∠ADE＝∠C B、∠AED＝∠B C、 $\frac{A D}{A B} = \frac{D E}{B C}$ D、 $\frac{A D}{A C} = \frac{A E}{A B}$

查看试题解析
3. 下面两个三角形一定相似的是（　　）

A、两个等腰三角形 B、两个直角三角形 C、两个钝角三角形 D、两个等边三角形

查看试题解析
4. 如图，已知∠1＝∠2＝∠3，则下列表达式正确的是（）

A、 $\frac{A B}{A D} = \frac{D E}{B C}$ B、 $\frac{A C}{A E} = \frac{A D}{A B}$ C、 $\frac{A B}{A C} = \frac{A D}{A E}$ D、 $\frac{B C}{D E} = \frac{A E}{A C}$

查看试题解析
5. 如图，在平面直角坐标系中，A（0，4），B（2，0），点C在第一象限，若以A、B、C为顶点的三角形与△AOB相似（不包括全等），则点C的个数是（　　）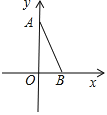

A、1 B、2 C、3 D、4

查看试题解析

6. 如图，P是正方形ABCD的边BC上一点，且BP＝3PC，Q是DC的中点，则AQ∶QP等于．

查看试题解析
7. 如图，在▱ABCD中，AB＝10，AD＝6，点E是AD的中点，在AB上取一点F，使△CBF与△CDE相似，则BF的长是．

查看试题解析
8. 如图，正方形ABCD中，E为AB的中点，AF⊥DE于点O，则 $\frac{A O}{D O}$ 等于

查看试题解析
9. 将一副三角板按图叠放，则△AOB与△DOC的面积之比等于

查看试题解析
10. 如图，正方形ABCD边长是2，BE＝CE，MN＝1，线段MN的端点M，N分别在CD，AD上滑动，当DM＝时，△ABE与以D，M，N为顶点的三角形相似．

查看试题解析

11. 已知，在△ABC中，三条边的长分别为2，3，4，△A′B′C′的两边长分别为1，1.5，要使△ABC∽△ $A^{'} B^{'} C^{'}$ ，求△ $A^{'} B^{'} C^{'}$ 中的第三边长．

查看试题解析
12. 如图，ABCD是平行四边形，点E在边BC延长线上，连AE交CD于点F，如果∠EAC=∠D，试问：AC•BE与AE•CD是否相等？

查看试题解析
13. 如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ACB和△DCE的顶点都在格点上，ED的延长线交AB于点F.

(1)、求证：△ACB∽△DCE；

(2)、求证：EF⊥AB.

查看试题解析
14. 如图，在△ABC和△ADE中， $\frac{A B}{A D} = \frac{B C}{D E} = \frac{A C}{A E}$ ，点B，D，E在一条直线上．求证：△ABD∽△ACE.

查看试题解析
15. 如图，在△ABC中（∠B≠∠C），AB=8 cm，BC=16 cm，点P从点A开始沿边AB向点B以2 cm/s的速度移动，点Q从点B开始沿边BC向点C以4 cm/s的速度移动，如果点P、Q分别从点A、B同时出发，经几秒钟△PBQ与△ABC相似？试说明理由.

查看试题解析

2018-2019学年数学北师大版九年级上册4.5 相似三角形判定定理的证明 同步练习