湖南省郴州六中2019届九年级上学期数学第一次月考试卷(湘教一、二章)
试卷更新日期:2018-11-08 类型:月考试卷
一、单选题
-
1. 下列式子中,表示 是 的反比例函数的是( )A、 B、 C、 D、2. 用配方法解一元二次方程 ,把左边写成完全平方形式后结果为( )
A、 B、 C、 D、3. 已知反比例函数 的图象如图,则一元二次方程 根的情况是( ) A、有两个不等实根 B、有两个相等实根 C、没有实根 D、无法确定4. 已知 是一元二次方程 的一个实数根,则 的取值范围为( )
A、有两个不等实根 B、有两个相等实根 C、没有实根 D、无法确定4. 已知 是一元二次方程 的一个实数根,则 的取值范围为( )
A、 B、 C、 D、5. 已知一次函数 的图象经过第一、二、四象限,则反比例函数 的图象在( )
A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限6. 若 ,则 的值为( )
A、 或 B、 或 3 C、 或 3 D、 或7. 双曲线 , 在第一象限的图象如图所示,其中 的解析式为 ,过 图象上的任意一点 ,作 轴的平行线交 图象于 ,交 轴于 ,若 ,则 的解析式是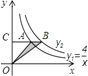 A、 B、 C、 D、8. 二次三项式 配方后变为( )
A、 B、 C、 D、8. 二次三项式 配方后变为( )
A、 B、 C、 D、9. 方程 的左边配成完全平方后所得方程为( )
A、 B、 C、 D、以上答案均不对10. 反比例函数 的图象位于
A、第一、三象限 B、第二、四象限 C、第一、四象限 D、第二、三象限二、填空题
-
11. 如图,已知 , 为反比例函数 图象上的两点,动点 在 轴正半轴上运动,当线段 与线段 之差达到最大时,点 的坐标是 .
 12. 如果关于 的方程 没有实数根,那么 的最大整数值是 .
12. 如果关于 的方程 没有实数根,那么 的最大整数值是 .
13. 过 点的反比例函数关系式是 .
14. 已知 ,那么 .
15. 若一次函数 的图像与反比例函数 的图像没有公共点,则实数 的取值范围是.
16. 在 中, , , ,动点 从 开始向 以 速度移动,点 从 开始向 以 的速度移动,点 到 后停止,点 到 后停止,则能使 面积为 的时间为 .
17. 一定质量的氧气,它的密度 是它的体积 的反比例函数.当 时, ,则 与 的函数关系是 .
18. 已知反比例函数 的图象一支位于第一象限,图象的另一分支位于象限, 常数取值范围 , 在这个函数上两点 , ,则 (填“ ”“ ”或“ ”)
19. 有一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度 (单位: )是体积 (单位: )的反比例函数,它的图象如图所示,当 时,气体的密度是 . 20. 已知反比例函数 的图象在二、四象限,则 可取 . (符合条件一个即可)
20. 已知反比例函数 的图象在二、四象限,则 可取 . (符合条件一个即可)
三、解答题
-
21. 解方程
(1)、 .
(2)、
(3)、 .22. 如图,点 是双曲线 第二象限上的点,且 ,在这条双曲线第二象限上有点 ,且 的面积为 ,求点 的坐标. 23. 如图,在直角坐标系 中,直线 与双曲线 相交于 、 两点, 轴,垂足为 , 的面积是 .
23. 如图,在直角坐标系 中,直线 与双曲线 相交于 、 两点, 轴,垂足为 , 的面积是 . (1)、求 、 的值;
(1)、求 、 的值;
(2)、求 的面积.24. 某电商销售一款时装,进价 元/件,售价 元/件,每天销售 件,每销售一件需缴纳平台推广费 元.该电商计划开展降价促销活动,通过市场调研发现,该时装售价每降 元,每天销量增加 件.为保证市场稳定,供货商规定售价不得低于 元/件.问该电商对这款时装的每件售价定为多少元才能使每天扣除平台推广费之后的利润达到 元?
25. 如图,一次函数 和反比例函数 交于点 . (1)、求反比例函数和一次函数的解析式;(2)、求 的面积;(3)、根据图象写出一次函数的值大于反比例函数的值的 的取值范围.26. 心理学研究发现,一般情况下,在一节 分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数 随时间 (分钟)的变化规律如下图所示(其中 、 分别为线段, 为双曲线的一部分).
(1)、求反比例函数和一次函数的解析式;(2)、求 的面积;(3)、根据图象写出一次函数的值大于反比例函数的值的 的取值范围.26. 心理学研究发现,一般情况下,在一节 分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数 随时间 (分钟)的变化规律如下图所示(其中 、 分别为线段, 为双曲线的一部分).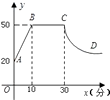 (1)、求注意力指标数 与时间 (分钟)之间的函数关系式;
(1)、求注意力指标数 与时间 (分钟)之间的函数关系式;
(2)、开始学习后第 分钟时与第 分钟时相比较,何时学生的注意力更集中?
(3)、某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知;自主探索,合作交流;总结归纳,巩固提高”.其中“教师引导,回顾旧知”环节 分钟;重点环节“自主探索,合作交流”这一过程一般需要 分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于 .请问这样的课堂学习安排是否合理?并说明理由.