湖南省郴州六中2019届九年级上学期数学第一次月考试卷
试卷更新日期:2018-11-08 类型:月考试卷
一、单选题
-
1. 下列函数是反比例函数的是( )
A、 B、y= C、y=x²+2x D、y=4x+82. 用配方法将方程 变形得( )
A、(x-6)²=41 B、(x-3)²=4 C、(x-3)²=14 D、(x-6)²=363. 小明乘车从南充到成都,行车的速度 和行车时间 之间的函数图象是( )
A、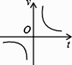 B、
B、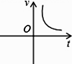 C、
C、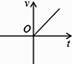 D、
D、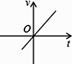 4. 关于 的一元二次方程 的一个根是 ,则 的值( )
4. 关于 的一元二次方程 的一个根是 ,则 的值( )
A、-2 B、2 C、2或-2 D、05. 如图,在直角坐标系中,正方形的中心在原点 ,且正方形的一组对边与 轴平行,点 是反比例函数 的图象上与正方形的一个交点,若图中阴影部分的面积等于 ,则 的值为( )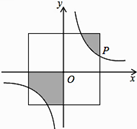 A、16 B、1 C、4 D、-166. 方程 的解是( )
A、16 B、1 C、4 D、-166. 方程 的解是( )
A、3 B、3,-1 C、-1 D、-3,17. 下列说法正确的是( )
A、等腰三角形的角平分线、中线、高线互相重合 B、面积相等的两个三角形一定全等 C、用反证法证明命题“三角形中至少有一个角不大于 ”的第一步是“假设三角形中三个角都大于 ” D、反比例函数 中函数值 随自变量 的增大一定而减小8. 如果一元二次方程 能用公式法求解,那么必须满足的条件是( )
A、b²-4ac≥0 B、b²-4ac≤0 C、b²-4ac>0 D、b²-4ac<09. 如图、点 为双曲线上一点, 轴, ,则双曲线的解析式为( )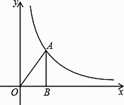 A、 B、 C、 D、10. 用配方法将二次三项式 变形的结果是( )
A、 B、 C、 D、10. 用配方法将二次三项式 变形的结果是( )
A、(a-1)²+1 B、(a+1)²+1 C、(a+1)²-1 D、(a-1)²-1二、填空题
-
11. 已知反比例函数 的图象上有两点 , 且 ,则 (填“ ”,“ ”或“ ”)
12. 关于x的一元二次方程 有两个不相等的实数根,则 的取值范围是.
13. 已知反比例函数的图象经过点 ,则这个函数的表达式是 .
14. 已知关于 的方程 的两根分别是 和 ,则 .
15. 某班有一人患了流感,经过两轮传染后,班上有 人被传染患上了流感,按这样的传染速度,若 人患了流感,则第一轮传染后患上流感的人数是 .
16. 方程 的解是 .
17. 有一面积为120的梯形,其上底是下底长的 ,若上底长为x,高为y,则y与x的函数关系式为 ;当高为10时,x=.
18. 若关于x的一元二次方程 没有实数根,则k的取值范是 .
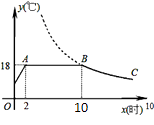
19. 我们知道,比较两个数的大小有很多方法,其中的图象法也非常巧妙,比如,通过图中的信息,我们可以得出 的解是 .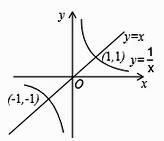 20. 某种蓄电池的电压为定值,使用此电源时,电流 与可变电阻 之间的函数关系如图所示,当用电器的电流为 时,用电器的可变电阻为 .
20. 某种蓄电池的电压为定值,使用此电源时,电流 与可变电阻 之间的函数关系如图所示,当用电器的电流为 时,用电器的可变电阻为 .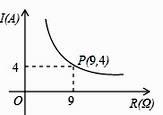
三、解答题
-
21. 用恰当的方法解下列方程:
① ;
② ;
③ ;
④ ;
22. 如图双曲线 与矩形 AOCB 的边 AB 、 BC 分别交于 E 、 F 点, OA 、 OC 在坐标轴上,BE=2AE 且S四边形OEBF=2,求 k . 23. 已知关于 的一元二次方程方程 有两个不相等的实数根.
23. 已知关于 的一元二次方程方程 有两个不相等的实数根.
(1)、求 的取值范围;
(2)、当 取最大整数时,不解方程直接写出方程的两根之和与两根之积.
24. 如图,在 中, , , ,点 、 同时由 、 两点出发分别沿 、 向点 匀速移动,它们的速度都是 米/秒,问:几秒后 的面积为 面积的一半?