江苏省宜兴市周铁学区2018-2019学年八年级上学期数学第一次月考试卷
试卷更新日期：2018-11-08 类型：月考试卷
一、单选题
-
1. 下列四个图案是我国几家银行的标志，其中是轴对称图形的有（ ）
A、1个 B、2个 C、3个 D、4个2. 用尺规作图，不能作出唯一直角三角形的是（ ）A、已知两条直角边 B、已知两个锐角 C、已知一直角边和直角边所对的一锐角 D、已知斜边和一直角边3. 下列语句中正确的有几个（ ）①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③两个轴对称图形的对应点一定在对称轴的两侧；④一个圆有无数条对称轴．
A、1 B、2 C、3 D、44. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的（ ）
A、CB=CD B、
BAC= DAC
C、 BCA= DCA
D、 B= D=900
5. 如图，请仔细观察用直尺和圆规作一个角 等于已知角 的示意图，请你根据所学的图形的全等这一章的知识，说明画出 的依据是（ ）
A、 B、 C、 D、6. 如图，将三角形纸片ABC折叠，使点C与点A重合，折痕为DE. 若∠B＝80°，∠BAE＝26°，则∠EAD的度数为（ ）
A、36° B、37° C、38° D、45°7. 如图所示，将一个正方形纸片对折两次，然后再上面打3个洞，则纸片展开后是（ ）
A、
B、
C、
D、
8.如图，工人师傅做了一个长方形窗框ABCD，E、F、G、H分别是四条边上的中点，为了使它稳固，需要在窗框上钉一根木条，这根木条不应钉在（ ）
A、A，C两点之间 B、E，G两点之间 C、B，F两点之间 D、G，H两点之间9. 如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是28cm2 ， AB=20cm，AC=8cm，则DE的长是（ ）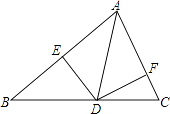
A、4cm B、3cm C、2cm D、1cm10. 如图，在△ABC中，AB=BC，∠ACB=90°，点D，E在AB上，将△ACD、△BCE分别沿CD、CE翻折，点A，B分别落在点A′、B′的位置，再将△A′CD、△B′CE分别沿A′C，B′C翻折，点D与点E恰好重合于点O，则∠A′OB′的度数是（ ）
A、90° B、120° C、135° D、150°二、填空题
-
11. 下列图形：①角；②直角三角形；③等边三角形；④线段；⑤等腰三角形；⑥平行四边形.其中一定是轴对称图形的有个.
12. 小明从平面镜中看到镜子对面电子钟示数如图所示，这时的时刻应是 ．
13. 如图，AC=BD，要使ΔABC≌ΔDCB，只要添加一个条件.
14. 如图9， △ABC的周长是32，且BD=DC，AD⊥BC于D，△ACD的周长为24，那么AD的长为。
15. 如图，已知AB//CF，E为DF的中点，若AB＝8 cm，BD＝3 cm，则CF＝cm．
16. 如图，点D在边BC上，DE⊥AB，DF⊥BC，垂足分别为点E，D，BD＝CF，BE＝CD．若∠AFD＝155°，则∠EDF＝ ．
17. 如图，方格纸中△ABC的3个顶点分别在小正方形的顶点（格点）上，这样的三角形叫格点三角形，
图中与△ABC全等的格点三角形共有个（不含△ABC）．
18. 已知在△ABC中，AB=5，BC=7，BM是AC边上的中线，则BM的取值范围为 ．
三、解答题
-
19. 如图，在3×3的正方形网格中，有一个以格点为顶点的三角形.
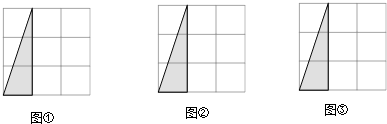(1)、请你在图①，图②，图③中，分别画出一个与该三角形成轴对称且以格点为顶点的三角形，并将所画三角形涂上阴影．（注：所画的三幅图不能重复）．
(2)、格纸中所有与该三角形成轴对称且以格点为顶点的三角形共有个．
20. 如图，在所给正方形网格图中完成下列各题：
(1)、画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1 ；
(2)、在DE上画出点Q，使△QAB的周长最小.
21. 已知△ABC，按下列要求作图：（尺规作图，保留痕迹不写作法。）
①作△ABC的角平分线BE，交AC于点E；
②作BC边上的高AD，垂足为D．
22. 如图，点A、E、F、C在同一条直线上，AD∥BC，AD=CB，AE=CF．求证：BE=DF．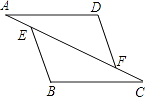
23. 两块完全相同的三角形纸板ABC和DEF，按如图所示的方式叠放，阴影部分为重叠部分，点O为边AC和DF的交点.不重叠的两部分△AOF与△DOC是否全等？为什么？
24. 如图（1）△ABC中，H是高AD和BE的交点，且AD=BD．
(1)、请你猜想BH和AC的关系，并说明理由；(2)、若将图（1）中的∠A改成钝角，请你在图（2）中画出该题的图形，此时（1）中的结论还成立吗？（不必证明）．
25. 在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
(1)、如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=°；(2)、设∠BAC=α，∠BCE=β．①如图2，当点D在线段BC上移动，则α与β有怎样的数量关系？请说明理由；
②当点D在直线BC上移动，则α与β有怎样的数量关系？请直接写出你的结论．
26. 如图，已知长方形ABCD中，AD＝6cm，AB＝4cm，点E为AD的中点．若点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BC上由点B向点C运动．
(1)、若点Q的运动速度与点P的运动速度相等，经过1秒后，△AEP与△BPQ是否全等，请说明理由，并直接写出此时线段PE和线段PQ的位置关系；(2)、若点Q的运动速度与点P的运动速度相等，运动时间为t秒，设△PEQ的面积为Scm2 ， 请用t的代数式表示S；(3)、若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△AEP与△BPQ全等？