江苏省句容市二中片区合作共同体2018-2019学年八年级上学期数学第一次月考试卷
试卷更新日期:2018-11-08 类型:月考试卷
一、单选题
-
1. 下列图形是全等图形的是( )A、
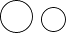 B、
B、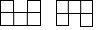 C、
C、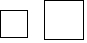 D、
D、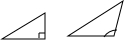 2. 如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
2. 如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( ) A、AB=DE B、DF∥AC C、∠E=∠ABC D、AB∥DE3. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A、AB=DE B、DF∥AC C、∠E=∠ABC D、AB∥DE3. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )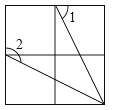 A、150° B、180° C、210° D、225°4. 如图,将两根钢条AA′、BB′的中点 O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A、150° B、180° C、210° D、225°4. 如图,将两根钢条AA′、BB′的中点 O连在一起,使AA′、BB′能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( ) A、SAS B、ASA C、SSS D、AAS5. 小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
A、SAS B、ASA C、SSS D、AAS5. 小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( ) A、21∶10 B、10∶21 C、10∶51 D、12∶016. 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A、21∶10 B、10∶21 C、10∶51 D、12∶016. 如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )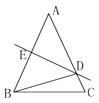 A、5cm B、10cm C、15cm D、17.5cm7. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A、5cm B、10cm C、15cm D、17.5cm7. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( ) A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确8. 如图,在 2×2 的正方形网格中,有一个格点△ABC(阴影部分),则网格中所有与△ABC成轴对称的格点三角形的个数为( )
A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确8. 如图,在 2×2 的正方形网格中,有一个格点△ABC(阴影部分),则网格中所有与△ABC成轴对称的格点三角形的个数为( ) A、2 B、3 C、4 D、59. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )A、
A、2 B、3 C、4 D、59. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )A、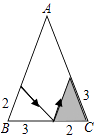 B、
B、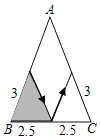 C、
C、 D、
D、 10. 如图,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为( )
10. 如图,已知五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=2,则五边形ABCDE的面积为( ) A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 在字母A、B、C、D、E、F、G、H、I、J中不是轴对称图形的有个.12. 如图所示,已知△ABC≌△DFE,AB=4cm,BC=6cm,AC=5cm,CF=2cm,∠A=70°,∠B=65°,则∠D=°,∠F=°,DE= , BE= .
 13. 如图,根据作图痕迹可知∠ADC=°.
13. 如图,根据作图痕迹可知∠ADC=°. 14. 若△ABC≌△A′B′C′,AB=24,S△A′B′C′=180,则△ABC的AB边上的高是 .15. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
14. 若△ABC≌△A′B′C′,AB=24,S△A′B′C′=180,则△ABC的AB边上的高是 .15. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= . 16. 如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为 .
16. 如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为 . 17. 如图所示,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是.
17. 如图所示,在△ABC中,∠B=∠C=50°,BD=CF,BE=CD,则∠EDF的度数是.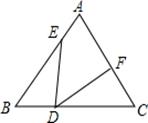 18. 已知△ABC中,AB=BC≠AC,作与△ABC只有一条公共边,且与△ABC全等的三角形,这样的三角形一共能作出个.19. 如图,已知点P为∠AOB的角平分线上的一定点,D是射线OA上的一定点,E是OB上的某一点,满足PE=PD,则∠OEP与∠ODP的数量关系是 .
18. 已知△ABC中,AB=BC≠AC,作与△ABC只有一条公共边,且与△ABC全等的三角形,这样的三角形一共能作出个.19. 如图,已知点P为∠AOB的角平分线上的一定点,D是射线OA上的一定点,E是OB上的某一点,满足PE=PD,则∠OEP与∠ODP的数量关系是 . 20. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时.△ABP和△DCE全等.
20. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为秒时.△ABP和△DCE全等.
三、解答题
-
21. 如图,阴影部分是由5个小正方形组成的一个直角图形,请用二种方法分别在下图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
 22. 如图,AE⊥BD,CF⊥BD,AE=CF,BF=DE.
22. 如图,AE⊥BD,CF⊥BD,AE=CF,BF=DE.求证:AB∥CD.
 23. 某种产品的商标如图所示,O是线段AC、BD的交点,并且AO=DO.请你在不作辅助线的情况下添加一个条件,证明△ABO和△DCO全等.
23. 某种产品的商标如图所示,O是线段AC、BD的交点,并且AO=DO.请你在不作辅助线的情况下添加一个条件,证明△ABO和△DCO全等.
添加条件
证明:
24. 如图,在 中, . (1)、用圆规和直尺在边 上作点 ,使点 到 的距离相等(保留作图痕迹,不写作法和证明过程);(2)、当满足(1)的点 到 的距离相等时,求 的度数.
(1)、用圆规和直尺在边 上作点 ,使点 到 的距离相等(保留作图痕迹,不写作法和证明过程);(2)、当满足(1)的点 到 的距离相等时,求 的度数.
25. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:DE=AF. 26. 如图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=3m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2m,点A到地面的距离AE=1.8m;当他从A处摆动到A′处时,有A'B⊥AB.
26. 如图是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD上,转轴B到地面的距离BD=3m.小亮在荡秋千过程中,当秋千摆动到最高点A时,测得点A到BD的距离AC=2m,点A到地面的距离AE=1.8m;当他从A处摆动到A′处时,有A'B⊥AB. (1)、求A′到BD的距离;(2)、求A′到地面的距离.
(1)、求A′到BD的距离;(2)、求A′到地面的距离.

