湘教版八年级数学上册2.5.3“角边角”(ASA) 同步练习
试卷更新日期:2018-11-08 类型:同步测试
一、选择题
-
1.
如图,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小、形状完全相同的玻璃,那么他可以( )
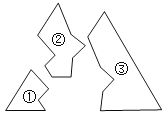 A、带①去 B、带②去 C、带③去 D、带①和②去2. 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
A、带①去 B、带②去 C、带③去 D、带①和②去2. 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( ) A、SAS B、ASA C、AAS D、SSS3. 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使 ,再作出BF的垂线DE,使A、C、E在同一条直线上 如图 ,可以证明在 ≌ ,得 ,因此,测得DE的长就是AB的长,在这里判定在 ≌ 的条件是( )
A、SAS B、ASA C、AAS D、SSS3. 要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使 ,再作出BF的垂线DE,使A、C、E在同一条直线上 如图 ,可以证明在 ≌ ,得 ,因此,测得DE的长就是AB的长,在这里判定在 ≌ 的条件是( ) A、ASA B、SAS C、SSS D、HL4. 如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA'=∠CBA,∠BCA'=∠BCA.可得△A'BC≌△ABC,所以A'B=AB,所以测量A'B的长即可得AB的长.判定图中两个三角形全等的理由是( )
A、ASA B、SAS C、SSS D、HL4. 如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作∠CBA'=∠CBA,∠BCA'=∠BCA.可得△A'BC≌△ABC,所以A'B=AB,所以测量A'B的长即可得AB的长.判定图中两个三角形全等的理由是( ) A、SAS B、ASA C、SSS D、AAS5. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的是( )
A、SAS B、ASA C、SSS D、AAS5. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中一定和△ABC全等的是( ) A、甲、乙 B、甲、丙 C、乙、丙 D、乙
A、甲、乙 B、甲、丙 C、乙、丙 D、乙二、填空题
-
6. 如图所示,两个三角形全等,其中已知某些边的长度和某些角的度数,则x= .
 7. 如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是 . (填写一个即可,不得添加辅助线和字母)
7. 如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是 . (填写一个即可,不得添加辅助线和字母)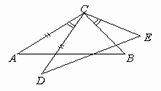 8. 如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m,则河宽为。
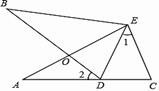
8. 如图,小李为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m,则河宽为。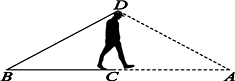 9. 如图,∠1=∠2.
9. 如图,∠1=∠2.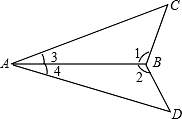 (1)、当BC=BD时,△ABC≌△ABD的依据是;(2)、当∠3=∠4时,△ABC≌△ABD的依据是 .
(1)、当BC=BD时,△ABC≌△ABD的依据是;(2)、当∠3=∠4时,△ABC≌△ABD的依据是 .三、解答题
-
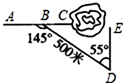
10. 如图所示,施工队在沿AC方向开山修路,为了加快施工进度,要在小山的另一边点E同时施工,从AC上的一点B,取 , 米, ,要使A,C,E成一直线,那么开挖点E离点B的距离如何求得?请你设计出解决方案.