湘教版八年级数学上册2.5.2“边角边”（SAS） 同步练习
试卷更新日期：2018-11-08 类型：同步测试
一、选择题
-
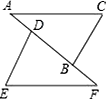
1. 如图， ， ，判定 ≌ 的依据是（ ）
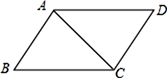A、SSS B、SAS C、ASA D、HL2. 如图，由∠1=∠2，BC=DC，AC=EC，得△ABC≌△EDC的根据是（ ）
A、SAS B、ASA C、AAS D、SSS3. 下列两个三角形的对应元素中，不能判断两个三角形全等的是（ ）A、SSA B、AAS C、SAS D、ASA4. 如图，AC、BD相交于点O，∠1=∠2，若用“SAS”说明△ACB≌△BDA，则还需要加上条件（ ）
A、AD=BC B、BD=AC C、∠D=∠C D、OA=AB5. 如图：如果OA=OD，用“SAS”说明△AOB≌△DOC，还需（ ）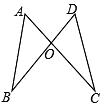
A、AB=DC B、∠A=∠D C、OB=OC D、∠A=∠E二、填空题
-
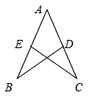
6. 如图，根据SAS，如果AB＝AC，只要满足 ，即可判定ΔABD≌ΔACE。
7. 把两根钢条A′B、AB′的中点连在一起，可以做成一个测量工件内槽宽工具（卡钳），如图，若得AB=6厘米，则槽宽为厘米．
8. 如图，已知 ， ，要使 ≌ ，若以“SAS”为依据，补充的条件是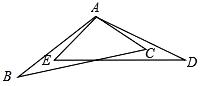
9. 如图，已知BD=CD，∠1=∠2；则△ABD≌△ACD，理由是：（已知）
（已知）
（公共边）
则△ABD≌△ACD（SAS）
三、解答题
