黑龙江省牡丹江市管理局北斗星协会2018届数学中考二模试卷
试卷更新日期:2018-11-08 类型:中考模拟
一、单选题
-
1. 下列各式运算中正确的是 ( )A、 B、 C、 D、2. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 某校初三7名学生中考体育测试成绩如下(单位:分):13.11.14.15.11.13.11,这组数据的众数和中位数分别为 ( )A、13,14 B、11,13 C、13,15 D、11,154. 下图是由7个完全相同的小立方块搭成的几何体,那么这个几何体的主视图是( )
3. 某校初三7名学生中考体育测试成绩如下(单位:分):13.11.14.15.11.13.11,这组数据的众数和中位数分别为 ( )A、13,14 B、11,13 C、13,15 D、11,154. 下图是由7个完全相同的小立方块搭成的几何体,那么这个几何体的主视图是( ) A、
A、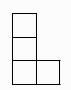 B、
B、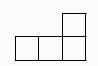 C、
C、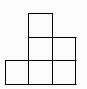 D、
D、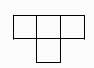 5. 如图所示,四边形ABCD是边长为4cm的正方形,动点P在正方形ABCD的边上沿着A→B→C→D的路径以1cm/s的速度运动,在这个运动过程中△APD的面积s(cm2)随时间t(s)的变化关系用图象表示,正确的是( )
5. 如图所示,四边形ABCD是边长为4cm的正方形,动点P在正方形ABCD的边上沿着A→B→C→D的路径以1cm/s的速度运动,在这个运动过程中△APD的面积s(cm2)随时间t(s)的变化关系用图象表示,正确的是( )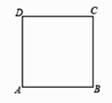 A、
A、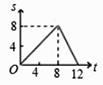 B、
B、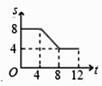 C、
C、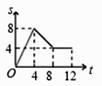 D、
D、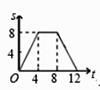 6. 如图,反比例函数与正比例函数的图象交于A、B两点,过点A作AC⊥x轴于点C.若△ABC的面积是4,则这个反比例函数的解析式是( )
6. 如图,反比例函数与正比例函数的图象交于A、B两点,过点A作AC⊥x轴于点C.若△ABC的面积是4,则这个反比例函数的解析式是( ) A、y= B、y= C、y= D、y=7. 如图,圆锥形烟囱帽的底面直径为80cm,母线长为50cm,则这样的烟囱帽的侧面积是( ).
A、y= B、y= C、y= D、y=7. 如图,圆锥形烟囱帽的底面直径为80cm,母线长为50cm,则这样的烟囱帽的侧面积是( ). A、4000πcm2 B、3600πcm2 C、2000πcm2 D、1000πcm28. 如图,在▱ABCD中,点M为CD中点,AM 与BD相交于点 N,那么S△DM N∶S▱ABCD为 ( )
A、4000πcm2 B、3600πcm2 C、2000πcm2 D、1000πcm28. 如图,在▱ABCD中,点M为CD中点,AM 与BD相交于点 N,那么S△DM N∶S▱ABCD为 ( ) A、1∶12 B、1∶9 C、1∶8 D、1∶69. 某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位,要求租用的车辆不留空座,也不能超载。租车方案有( )A、4种 B、3种 C、2种 D、1种10. 如图,已知 平行四边形ABCD中, , 于 , 于 , 相交于 , 的延长线相交于 ,下面结论:① ② ③ ④ 其中正确的结论的个数是( )
A、1∶12 B、1∶9 C、1∶8 D、1∶69. 某班组织20名同学去春游,同时租用两种型号的车辆,一种车每辆有8个座位,另一种车每辆有4个座位,要求租用的车辆不留空座,也不能超载。租车方案有( )A、4种 B、3种 C、2种 D、1种10. 如图,已知 平行四边形ABCD中, , 于 , 于 , 相交于 , 的延长线相交于 ,下面结论:① ② ③ ④ 其中正确的结论的个数是( )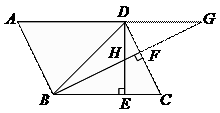 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
11. 科技兴国,国之利器。截至2017年底,我国高铁已经建成运营的里程约为2.5万公里,占全世界超过六成,居世界第一位。其中2.5万公里用科学记数法表示为 公里。12. 如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件使四边形AECF是平行四边形(只填一个即可).
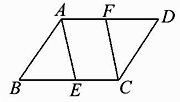 13. 把一副普通扑克牌中的13张红桃洗匀后正面向下,从中任意抽取一张,抽出的牌的点数是4的倍数的概率是。14. 若不等式 组 有3个整数解,则a的取值范围是。15. 某商店老板将一件进价为800元的商品先提价 ,再打8折卖出,则卖出这件商品所获利润是元.16. 如图,点A、B、C、D分别是⊙O上四点,∠ABD=20°,BD是直径,则∠ACB=。
13. 把一副普通扑克牌中的13张红桃洗匀后正面向下,从中任意抽取一张,抽出的牌的点数是4的倍数的概率是。14. 若不等式 组 有3个整数解,则a的取值范围是。15. 某商店老板将一件进价为800元的商品先提价 ,再打8折卖出,则卖出这件商品所获利润是元.16. 如图,点A、B、C、D分别是⊙O上四点,∠ABD=20°,BD是直径,则∠ACB=。 17. 已知关于 的分式方程 无解,则 的值是 .18. 矩形ABCD中,AB=20,BC=6,E为AB边的中点,P为CD边上的点,且△AEP是腰长为10的等腰三角形,则线段BP的长为19. 如图,等腰直角三角形 直角边长为1,以它的斜边上的高 为腰,做第一个等腰直角三角形 ,其面积为S1;再以所做的第一个等腰直角三角形 的斜边上的高 为腰,做第二个等腰直角三角形 ;……以此类推,这样所做的第7个等腰直角三角形的面积S7= .
17. 已知关于 的分式方程 无解,则 的值是 .18. 矩形ABCD中,AB=20,BC=6,E为AB边的中点,P为CD边上的点,且△AEP是腰长为10的等腰三角形,则线段BP的长为19. 如图,等腰直角三角形 直角边长为1,以它的斜边上的高 为腰,做第一个等腰直角三角形 ,其面积为S1;再以所做的第一个等腰直角三角形 的斜边上的高 为腰,做第二个等腰直角三角形 ;……以此类推,这样所做的第7个等腰直角三角形的面积S7= .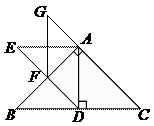
三、解答题
-
20. 先化简,再求值:( - )÷ , 然后选取一个你喜欢的数代入求值.21. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,点 的坐标为 .

①把 向上平移5个单位后得到对应的 ,画出 ,并写出 的坐标;
②以原点. .为对称中心,画出 与关于原点. .对称的 ,并写出点 的坐标.
③以原点O为旋转中心,画出把 顺时针旋转90°的图形△A3B3C3 , 并写出C3的坐标.
22. 如图,已知二次函数y= -x2+bx+c的图像经过A(2,0),B(0,-6)两点。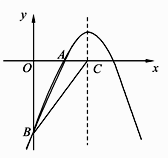 (1)、.求二次函数的解析式;(2)、.若该二次函数的图象对称轴与x轴交于点C,连接BA,BC,求△ABC的面积。
(1)、.求二次函数的解析式;(2)、.若该二次函数的图象对称轴与x轴交于点C,连接BA,BC,求△ABC的面积。
23. 某校组织了以“美好家园,你我共建;节能减排,人人有责”为主题的电子小报制作比赛,评分结果有60.70.80.90.100五种。现从中随机抽取部分作品,对其份数及成绩进行整理,制作如下两幅不完整的统计图。根据图中提供的信息,解答下列问题: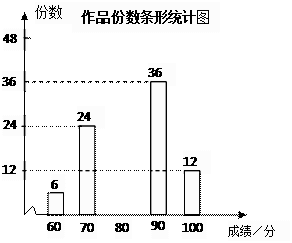
 (1)、本次抽取了多少份作品(2)、补全两幅统计图
(1)、本次抽取了多少份作品(2)、补全两幅统计图
(3)、已知该校收取参赛作品共600份,请估计该校比赛成绩达到90分以上(含90分)的作品有多少份?
24. A.B两地之间有一条笔直的公路,甲车从A地出发匀速向B地行驶,中途因有事停留了1小时后按原速驶向B地;在甲车出发的同时乙车从B地出发匀速向A地行驶,到达A地后,立即按原路原速返回到B地。两车在行驶的过程中,甲乙两车距A地的路程y(千米)与行驶时间x(小时)之间的函数关系式如图所示,请结合图像回答下列问题: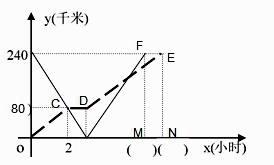 (1)、在图像的()中填入正确的数值(2)、求甲车在中途因事停留后驶向B地过程中,y与x之间的函数关系式
(1)、在图像的()中填入正确的数值(2)、求甲车在中途因事停留后驶向B地过程中,y与x之间的函数关系式
(3)、直接写出:乙车从A地出发多少小时后,甲.乙两车分别到甲车中途停留地的距离相等?
25. 在平面内有一等腰直角三角板(∠ACB=90º)和直线l.过点C作CE⊥l于点E,过点B作BF⊥l于点F.当点E与点A重合时(图①),易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图②.图③的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,请直接写出线段AF.BF.CE之间的数量关系的猜想(不需证明).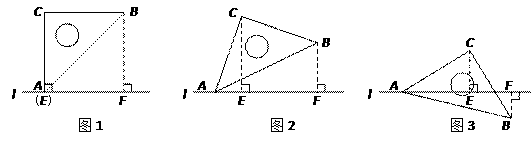 26. 为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价l80元,售价320元;乙种服装每件进价l50元,售价280元.(1)、若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?(2)、该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?
26. 为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价l80元,售价320元;乙种服装每件进价l50元,售价280元.(1)、若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?(2)、该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?
(3)、在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0<a<20)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?27. 在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3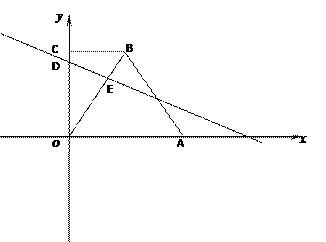 (1)、直接写出点B的坐标(2)、已知D.E分别为线段OC.OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式(3)、在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O.D.M.N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由。
(1)、直接写出点B的坐标(2)、已知D.E分别为线段OC.OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式(3)、在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O.D.M.N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由。