黑龙江省龙东地区2018届数学中考模拟试卷(三)
试卷更新日期:2018-11-08 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、﹣4x8÷2x4=﹣3x2 B、2x•3x=6x C、﹣2x+x=﹣3x D、(﹣x3)4=x122. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、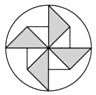 C、
C、 D、
D、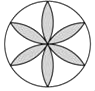 3. 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( )
3. 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 已知一组数据6,8,10,x的中位数与平均数相等,这样的x有( )A、1个 B、2个 C、3个 D、4个以上(含4个)5.
4. 已知一组数据6,8,10,x的中位数与平均数相等,这样的x有( )A、1个 B、2个 C、3个 D、4个以上(含4个)5.如图,矩形ABCD中,AB=1,BC=2,点P从点B出发,沿B→C→D向终点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数关系的图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 已知关于x的方程 有正根,则实数a的取值范围是( )A、a<0且a≠﹣3 B、a>0 C、a<﹣3 D、a<3且a≠﹣37. 如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且 ,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )
6. 已知关于x的方程 有正根,则实数a的取值范围是( )A、a<0且a≠﹣3 B、a>0 C、a<﹣3 D、a<3且a≠﹣37. 如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且 ,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为( )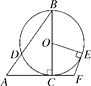 A、92° B、108° C、112° D、124°8. 如图,直线y=﹣x+3与y轴交于点A,与反比例函数y= (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
A、92° B、108° C、112° D、124°8. 如图,直线y=﹣x+3与y轴交于点A,与反比例函数y= (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( ) A、y= B、y=﹣ C、y= D、y=﹣9. 小华准备购买单价分别为4元和5元的两种拼装饮料,若小华将50元恰好用完,两种饮料都买,则购买方案共有( )A、2种 B、3种 C、4种 D、5种10. 如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:
A、y= B、y=﹣ C、y= D、y=﹣9. 小华准备购买单价分别为4元和5元的两种拼装饮料,若小华将50元恰好用完,两种饮料都买,则购买方案共有( )A、2种 B、3种 C、4种 D、5种10. 如图,在△ABC中,BC的垂直平分线交AC于点E,交BC于点D,且AD=AB,连接BE交AD于点F,下列结论:
①∠EBC=∠C;②△EAF∽△EBA;③BF=3EF;④∠DEF=∠DAE,其中结论正确的个数有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 据中国新闻网消息,今年高校毕业生人数将达到人,将数8200000用科学记数法表示为 .12. 在函数y= 中,自变量x的取值范围是 .13. 同时抛掷三枚质地均匀的硬币,出现两枚正面向上,一枚正面向下的概率是 .14. 若关于x的一元一次不等式组 无解,则m的取值范围为 .15. 某商品经过两次连续的降价,由原来的每件25元降为每件16元,则该商品平均每次降价的百分率为 .16. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=4,M是AB边上一动点,N是AC边上的一动点,则MN+MC的最小值为 .
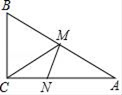 17. 已知圆锥底面圆的直径是20cm,母线长40cm,其侧面展开图圆心角的度数为 .18. 在Rt△ABC中,∠A=90°,AB=AC= +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为 .19. 如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1 , 再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第2018个正方形A2018B2018C2018D2018的周长是 .
17. 已知圆锥底面圆的直径是20cm,母线长40cm,其侧面展开图圆心角的度数为 .18. 在Rt△ABC中,∠A=90°,AB=AC= +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为 .19. 如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1 , 再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第2018个正方形A2018B2018C2018D2018的周长是 .
三、解答题
-
20. 先化简,再求值:( )÷ ,其中x=2sin45°.21. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
 (1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;(2)、若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标;(3)、在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.22. 如图,抛物线y=x2+bx+c与x轴交于A,B两点,且点A在点B的左侧,直线y=﹣x﹣1与抛物线交于A,C两点,其中点C的横坐标为2.
(1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;(2)、若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标;(3)、在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.22. 如图,抛物线y=x2+bx+c与x轴交于A,B两点,且点A在点B的左侧,直线y=﹣x﹣1与抛物线交于A,C两点,其中点C的横坐标为2. (1)、求二次函数的解析式;(2)、P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.
(1)、求二次函数的解析式;(2)、P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.
23. 在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: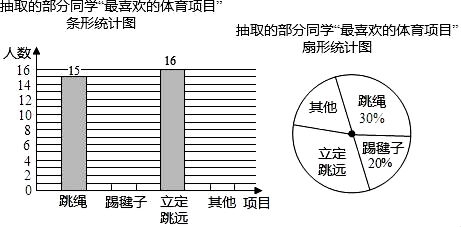 (1)、小龙一共抽取了名学生.(2)、补全条形统计图;(3)、求“其他”部分对应的扇形圆心角的度数.24. 小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题:
(1)、小龙一共抽取了名学生.(2)、补全条形统计图;(3)、求“其他”部分对应的扇形圆心角的度数.24. 小明从家出发沿滨江路到外滩公园徒步锻炼,到外滩公园后立即沿原路返回,小明离开家的路程s(单位:千米)与走步时间t(单位:小时)之间的函数关系如图所示,其中从家到外滩公园的平均速度是4千米/时,根据图形提供的信息,解答下列问题: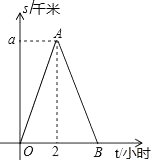 (1)、求图中的a值;
(1)、求图中的a值;
(2)、若在距离小明家5千米处有一个地点C,小明从第一次经过点C到第二次经过点C,所用时间为1.75小时,求小明返回过程中,s与t的函数解析式,不必写出自变量的取值范围;
(3)、在(2)的条件下,求小明从出发到回到家所用的时间.25. 在正方形ABCD中,过点B作直线l,点E在直线l上,连接CE,DE,CE=BC,过点C作CF⊥DE于点F,交直线l于点H,当l在如图①的位置时,易证:BH+EH= CH(不需证明).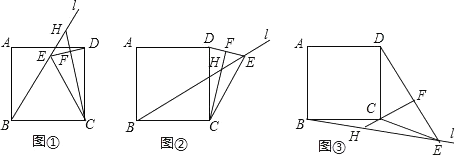 (1)、当l在如图②的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,并给予证明;(2)、当l在如图③的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,不必证明.26. 近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
(1)、当l在如图②的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,并给予证明;(2)、当l在如图③的位置时,线段BH,EH,CH之间有怎样的数量关系?写出你的猜想,不必证明.26. 近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:A型销售数量(台)
B型销售数量(台)
总利润(元)
5
10
2 000
10
5
2 500
(1)、每台A型空气净化器和B型空气净化器的销售利润分别是多少?(2)、该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;(3)、已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2 , 室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?27. 如图,在平面直角坐标系xOy中,矩形OABC的顶点B的坐标为(4,2),D是OA的中点,OE⊥CD交BC于点E,点P从点O出发,以每秒2个单位长度的速度沿射线OE运动.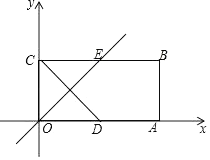 (1)、求直线OE的解析式;(2)、设以C,P,D,B为顶点的凸四边形的面积为S,点P的运动时间为t(单位:秒),求S关于t的函数解析式,并写出自变量t的取值范围;(3)、设点N为矩形的中心,则在点P运动过程中,是否存在点P,使以P,C,N为顶点的三角形是直角三角形?若存在,请直接写出t的值及点P的坐标;若不存在,请说明理由.
(1)、求直线OE的解析式;(2)、设以C,P,D,B为顶点的凸四边形的面积为S,点P的运动时间为t(单位:秒),求S关于t的函数解析式,并写出自变量t的取值范围;(3)、设点N为矩形的中心,则在点P运动过程中,是否存在点P,使以P,C,N为顶点的三角形是直角三角形?若存在,请直接写出t的值及点P的坐标;若不存在,请说明理由.