黑龙江省哈尔滨市道外区2018届九年级升学调研测试数学试卷
试卷更新日期:2018-11-08 类型:中考模拟
一、单选题
-
1. 的相反数数是( )A、2 B、-2 C、 D、2. 下列计算正确的是( )A、3m+3n=6mn B、y3÷y3=y C、a2·a3=a6 D、3. 下列图形中,是轴对称图形而不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 点A(-1,y1),B(-2,y2)在反比例函数y= 的图象上,则y1 , y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定5. 如图,是由五个相同的小正方体搭成的几何体,则它的左视图是( )
4. 点A(-1,y1),B(-2,y2)在反比例函数y= 的图象上,则y1 , y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、不能确定5. 如图,是由五个相同的小正方体搭成的几何体,则它的左视图是( )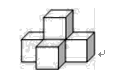 A、
A、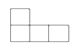 B、
B、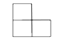 C、
C、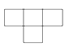 D、
D、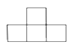 6. 一组数据从小到大排列为1,2,4,x,6,8.这组数据的中位数是5,那么这组数据的众数为( )
6. 一组数据从小到大排列为1,2,4,x,6,8.这组数据的中位数是5,那么这组数据的众数为( )
A、4 B、5 C、5.5 D、67. 跃进公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获利20%,则这种电子产品的标价为( )A、29元 B、28元 C、27元 D、26元8. 已知点M(2m-1,m-1)在第四象限,则m的取值范围在数轴上表示正确的是( )A、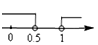 B、
B、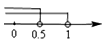 C、
C、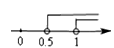 D、
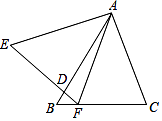
D、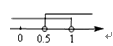 9. 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
9. 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:①∠C=∠E;②△ADE∽△FDB;③∠AFE=∠AFC;④FD=FB.其中正确的结论是( )
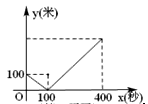
 A、①③ B、②③ C、①④ D、②④10. 甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:
A、①③ B、②③ C、①④ D、②④10. 甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:①甲的速度为5米/秒;②100秒时甲追上乙;③经过50秒时甲乙相距50米;④甲到终点时,乙距离终点300米.其中正确的说法有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
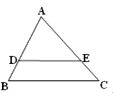
11. 一种病毒长度约为0.000056mm,用科学记数法表示这个数为.12. 比较大小:4 (填入“>”或“<”号)13. 函数y= 的自变量x的取值范围为 .14. 因式分解:2m2n﹣4mn+2n= .15. 不等式组 的解集为.16. 一个扇形的半径长为12cm,面积为24πcm2 , 则这个扇形的弧长为cm.17. 如图,在△ABC中,DE∥BC,若AB=5,BC=6,DE=4,则BD=.
 18. 如图,四边形ABCD内接于⊙O,延长CO交⊙O于点E,连接BE.若∠A=100°,∠E=60°,则∠ECD=°
18. 如图,四边形ABCD内接于⊙O,延长CO交⊙O于点E,连接BE.若∠A=100°,∠E=60°,则∠ECD=°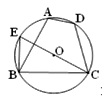 19. 在△ABC中,∠BAC=90°,AB=AC,点D在BC边上,把△ABD沿AD折叠后,使得点B落在点E处,连接CE,若∠DBE=20°,则∠ADC=.20. 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是9,则DP的长是 .
19. 在△ABC中,∠BAC=90°,AB=AC,点D在BC边上,把△ABD沿AD折叠后,使得点B落在点E处,连接CE,若∠DBE=20°,则∠ADC=.20. 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是9,则DP的长是 .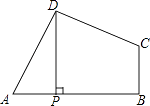
三、解答题
-
21. 先化简,再求值: ,其中a=2sin60°-3tan45°22. 图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
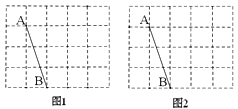 (1)、在图1中画出一个以AB为一边面积为 5的等腰RtABC,且点C在小正方形顶点上;
(1)、在图1中画出一个以AB为一边面积为 5的等腰RtABC,且点C在小正方形顶点上;
(2)、在图2中画出一个以AB为一边面积为 4的平行四边形ABDE,且点D和点E均在小正方形的顶点上;并直接写出所画四边形周长.23. 随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: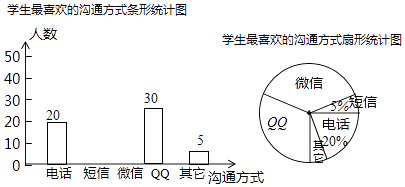 (1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?24. 如图,已知△ABC,AC的垂直平分线交AB于点D,交AC于点O,过点C作CE∥AB交直线OD于点E,连接AE、CD.
(1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?24. 如图,已知△ABC,AC的垂直平分线交AB于点D,交AC于点O,过点C作CE∥AB交直线OD于点E,连接AE、CD.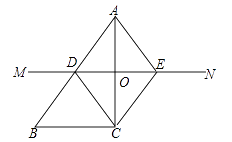 (1)、如图1,求证:四边形ADCE是菱形;(2)、如图2,当∠ACB=90°,BC=6,△ADC的周长为18时,求AC的长度.
(1)、如图1,求证:四边形ADCE是菱形;(2)、如图2,当∠ACB=90°,BC=6,△ADC的周长为18时,求AC的长度.
25. 飞马汽车销售公司3月份销售新上市一种新型低能耗汽车8辆,由于该型汽车的优越是经济适用性,销量快速上升,5月份该公司销售该型汽车达18辆.
(1)、求该公司销售该型汽车4月份和5月份的平均增长率;
(2)、该型汽车每辆的进价为9万元,该公司的该型车售价为9.8万元/辆.且销售m辆汽车,汽车厂返利销售公司0.04m万元/辆.若使6月份每辆车盈利不低于1.7万元,那么该公司6月份至少需要销售该型汽车多少辆?(盈利=销售利润+返利)
26. 如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.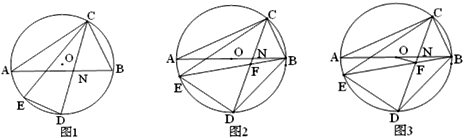 (1)、如图1,求证:∠AND=∠CED;(2)、如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°-∠DBE,求证:CD=CE;
(1)、如图1,求证:∠AND=∠CED;(2)、如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°-∠DBE,求证:CD=CE;
(3)、如图3,在⑵的条件下,连接OF,若BE=BD+4,BC= ,求线段OF的长.27. 如图,抛物线y=-(x+k)(x-5)交x轴于点A、B(A左B右),交y轴交于点C,BD⊥AC垂足为D,BD与OC交于点E,且CE=4OE.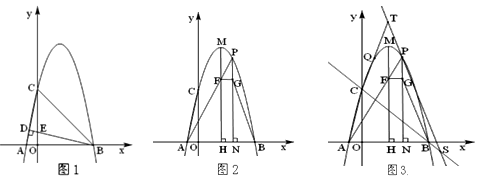 (1)、如图1,求抛物线的解析式;
(1)、如图1,求抛物线的解析式;
(2)、如图2,点M为抛物线的顶点,MH⊥x轴,垂足为H,点P为第一象限MH右侧抛物线上一点,PN⊥x轴于点N,PA交MH于点F,FG⊥PN于点G,求tan∠GBN的值;(3)、如图3,在⑵的条件下,过点P作BG的平行线交直线BC于点S,点T为直线PS上一点,TC交抛物线于点Q,若CQ=QT,TS= ,求点P的坐标.