浙江省宁波市2018-2019学年八年级上学期数学第一次月考试卷
试卷更新日期：2018-11-08 类型：月考试卷
一、选择题
-
1. 下列长度的三条线段，能组成三角形的是（ ）
A、4cm，5cm，9cm B、5cm，5cm，10cm C、8cm，8cm，15cm D、6cm，7cm，14cm2. 下列图案属于轴对称图形的是（ ）A、
B、
C、
D、
3. 在△ABC 中，∠A= ∠B= ∠ C，则此三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形4. 下列语句不是命题的是（ ）
A、两直线平行，同位角相等 B、若|a|=|b|，则 a=b C、作直线 AB 垂直于直线 CD D、同角的补角相等5. 如图一艘轮船由海平面上 A 地出发向南偏西 40°的方向行驶 40 海里到达 B 地，再由 B地向北偏西 20°的方向行驶 40 海里到达 C 地，则 A、C 两地相距（ ）
A、30 海里 B、40 海里 C、50 海里 D、60 海里6. 如图，一扇窗户打开后，用窗钩 AB 可将其固定，这里所运用的几何原理是（ ）
A、垂线段最短 B、两点之间线段最短 C、两点确定一条直线 D、三角形的稳定性7. 已知图中的两个三角形全等，则∠1等于（ ）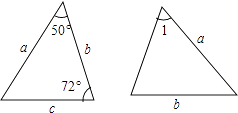
A、72° B、60° C、50° D、58°8. 对于命题“若 a2>b2 ， 则 a>b”，下面四组关于 a，b 的值中，能说明这个命题是假命题 的是（ ）
A、a=3，b=2 B、a=﹣1，b=3 C、a=﹣3，b=2 D、a=3，b=﹣19. 工人师傅常用角尺平分一个任意角，做法是：如图在∠AOB 的边OA，OB 上分别取 OM=ON， 然后移动角尺使角尺的两边相同的刻度分别与 M，N 重合，得到∠AOB 的平分线 OP， 做法中用到三角形全等的判定方法是（ ）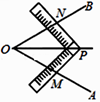
A、SSS B、SAS C、ASA D、AAS10. 如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（ ）
A、1 B、1.5 C、2 D、411. 下列三角形中，若 AB=AC，则能被一条直线分成两个小等腰三角形的是（ ）
A、①② B、①③ C、②③ D、②④12. 如图，在△ABC中，∠BAC 和∠ABC 的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D，下列四个结论：①∠AOB=900+ ∠C；②AE+BF=EF；③当∠C=90°时，E，F 分别是 AC，BC 的中点；④若OD=a，CE+CF=2b， 则 S△ CEF=ab．其中正确的是（ ）
A、①② B、①②③ C、①②④ D、①③④二、填空题
-
13. 把命题“等角的补角相等”改写成“如果„那么„”的形式是 ．
14. 如图，已知点E，F分别在 AB，AC上，且AE=AF，请补充一个条件： ， 使得△ABF≌△ACE．（只需填写一种情况即可）
15. 如图，△ABC 中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边BC上A1处，折痕为CD，则∠A1DB的度数为 ．
16. 若等腰三角形一腰上的中线把这个三角形的周长分成为12cm和21cm两部分，则这个等腰三角形的底边长为 ．
17. 如图，已知△ABC 的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=4，△ABC的面积是 ．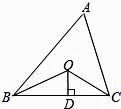
18. 如图，点O在直线m上，在m的同侧有A，B两点，∠AOB=90°，OA=10cm，OB=8cm，点P以2cm/s的速度从点 A 出发沿A—O—B 路径向终点 B 运动，同时点 Q 以1cm/s的速度从点B出发沿 B—O—A路径向终点A运动，两点都要到达相应的终点时才能停止运动．分别过点P，Q作PC⊥m于点 C，QD⊥m 于点C，QD⊥m于点D．若△OPC与△OQD全等，则点Q运动的时间是秒．
三、解答题
-
19. 如图，点 B，E，C，F 在一条直线上，AB=DE，AC=DF，BE=CF，求证：∠A=∠D．
20. 如图，在△ABC中，AD 是BC边上的高线，AE平分∠BAC，若∠BAC∶∠B∶∠C=4∶3∶2，求∠DAE 的度数．
21. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A，B，C 在小正方形的顶点上．
①在图中画出与△ABC关于直线1成轴对称的△A′B′C′；
②请直线l上找到一点P，使得 PC+PB 的距离之和最小．
22. 如图，点D，E在△ABC的BC边上，AB=AC，AD=AE．求证：BD=CE．
23. 如图，已知∠MAN，点B在射线AM上．
(1)、尺规作图（保留作图痕迹，不写作法）：①在 AN 上取点C，使 CB=CA；
②作∠BCN的平分线 CD；
(2)、在(1)的条件下，求证：AB∥CD．24. 把两个大小不同的含 45°角的直角三角板如图①放置，图②是由它抽象出的几何图形，点 B，C，E 在同一条直线上，连结 CD．求证：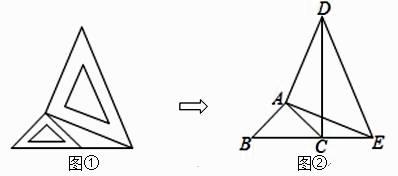
(1)、BE=CD；
(2)、DC⊥BE．25. 如图，△ABC中，AB=AC=2，∠B=40°．点D在线段 BC 上运动（点D不与B，C 重合），连接AD，作∠ADE=40°，DE 交线段AC于E．
(1)、当∠BAD=20°时，∠EDC=°；
(2)、当DC等于多少时，△ABD≌△DCE？并说明理由；(3)、在点D的运动过程中，△ADE的形状也在改变，判断 当∠BAD等于多少度时，△ADE是等腰三角形．
26. 在解决线段数量关系问题中，如果条件中有角平分线，经常采用下面构造全等 三角形的解决思路．如：在图1中，若C是∠MON的平分线OP上一点，点 A 在 OM 上，此时，在射线ON上截取 OB=OA，连结 BC，根据三角形全等的判定方法(SAS)，容易构 造出全等三角形△OBC 和△OAC，参考上面的方法，解答下列问题：
(1)、如图2，在△ABC 中，AD是∠BAC的平分线，E，F 分别为AB，AC上的点，且∠AED+∠AFD=180°．求证：DE=DF．
(2)、如图3，在非等边△ABC 中，∠B=60°，AD，CE 分别是∠BAC，∠BCA 的平分线，且AD，CE 交于点 F，求证：AC=AE+CD．