浙江省衢州市2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期:2018-11-08 类型:期中考试
一、单选题
-
1. 如图,已知 BF=CE,∠B=∠E,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
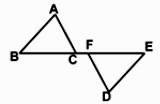 A、AB=DE B、AC∥DF C、∠A=∠D D、AC=DF2. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A、AB=DE B、AC∥DF C、∠A=∠D D、AC=DF2. 如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )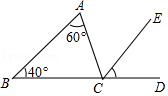 A、40° B、45° C、50° D、55°3. 不等式x+1≥2x﹣1的解集在数轴上表示为( )A、
A、40° B、45° C、50° D、55°3. 不等式x+1≥2x﹣1的解集在数轴上表示为( )A、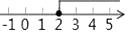 B、
B、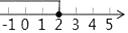 C、
C、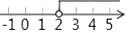 D、
D、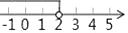 4. 已知 a>b,则下列不等式中,正确的是( )A、-3a>-3b B、 C、a-3>b-3 D、3-a>3-b5. 如图,在△ABC中,AB=AC,若以点B为圆心,BC长为半径作弧,交AC于点E,则下列结论一定正确的是( )
4. 已知 a>b,则下列不等式中,正确的是( )A、-3a>-3b B、 C、a-3>b-3 D、3-a>3-b5. 如图,在△ABC中,AB=AC,若以点B为圆心,BC长为半径作弧,交AC于点E,则下列结论一定正确的是( )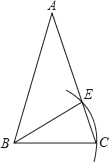 A、AE=BE B、BE是∠ABC的角平分线 C、∠A=∠EBC D、AE=BC6. 已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( )A、22 B、17 C、17或22 D、267. 下列说法中,正确的是( )A、直角三角形中,已知两边长为 3 和 4,则第三边长为 5 B、若一个三角形是直角三角形,其三边长为 a,b,c,则满足a2-b2=c2 C、以三个连续自然数为三边长不可能构成直角三角形 D、△ABC 中,若∠A∶∠B∶∠C=1∶5∶6,则△ABC 是直角三角形8. 如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则 BC 的长是( )
A、AE=BE B、BE是∠ABC的角平分线 C、∠A=∠EBC D、AE=BC6. 已知等腰三角形的一边长等于4,一边长等于9,则它的周长为( )A、22 B、17 C、17或22 D、267. 下列说法中,正确的是( )A、直角三角形中,已知两边长为 3 和 4,则第三边长为 5 B、若一个三角形是直角三角形,其三边长为 a,b,c,则满足a2-b2=c2 C、以三个连续自然数为三边长不可能构成直角三角形 D、△ABC 中,若∠A∶∠B∶∠C=1∶5∶6,则△ABC 是直角三角形8. 如图,AD⊥CD,CD=4,AD=3,∠ACB=90°,AB=13,则 BC 的长是( )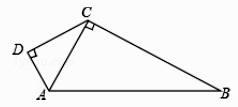 A、8 B、10 C、12 D、169. 如图,将两个大小、形状完全相同的△ABC 和△A′B′C′拼在一起,其中点 A′与点 A 重合,点 C′ 落在边 AB 上,连接 B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则 B′C 的长为( )
A、8 B、10 C、12 D、169. 如图,将两个大小、形状完全相同的△ABC 和△A′B′C′拼在一起,其中点 A′与点 A 重合,点 C′ 落在边 AB 上,连接 B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则 B′C 的长为( )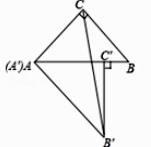 A、 B、6 C、 D、10. 如图,在△ABC 中,∠BAC 和∠ABC 的平分线相交于点 O,过点 O 作 EF∥AB 交 BC 于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
A、 B、6 C、 D、10. 如图,在△ABC 中,∠BAC 和∠ABC 的平分线相交于点 O,过点 O 作 EF∥AB 交 BC 于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
① ∠AOB=90°+ ②AE+BF=EF;③当∠C=90°时,E,F 分别是 AC,BC的中点;④若 OD=a,CE+CF=2b,则 S△CEF=ab其中正确的是( )
A、①② B、③④ C、①②④ D、①③④二、填空题
-
11. 命题“同位角相等”的逆命题是12. 如图,DE∥AB,则∠B 的大小为
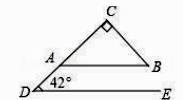 13. 将一副三角尺如图所示叠放在一起,若 AB=4 cm,则阴影部分的面积是cm2
13. 将一副三角尺如图所示叠放在一起,若 AB=4 cm,则阴影部分的面积是cm2 14. 如图为 6 个边长相等的正方形的组合图形,则∠1+∠2+∠3=°
14. 如图为 6 个边长相等的正方形的组合图形,则∠1+∠2+∠3=°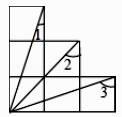 15. 不等式组: 的整数解为16. 若一个三角形三边长分别为 1.5,2,2.5,则这个三角形一定是三角形.
15. 不等式组: 的整数解为16. 若一个三角形三边长分别为 1.5,2,2.5,则这个三角形一定是三角形.
17. 关于 x 的不等式组 的整数解共有3个,则a的取值范围是18. 今年三月份甲、乙两个工程队承包了面积1800m2的区域绿化,已知甲队每天能完成100m2 , 需绿化费用为0.4万元;乙队每天能完成 50 m2 , 需绿化费用为 0.25万元,要使这次的绿化总费用不超过 8 万元,至少应安排甲队工作天三、解答题
-
19. 如图,在△ABC 和△DEF 中,点 B、F、C、E 在同一直线上,BF=CE,AC∥DF 且 AC=DF. 求证:AB∥DE.
 20. 解不等式组 并把解集在数轴上表示出来
20. 解不等式组 并把解集在数轴上表示出来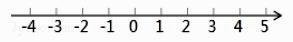 21. 如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
21. 如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.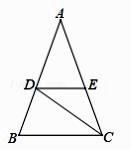 (1)、求证:DE=CE.(2)、若∠CDE=35°,求∠A 的度数.22. 已知:如图,在△ABC、△ADE 中,∠BAC=∠DAE=90°,AB=AC,AD=AE, 点 C、D、E 三点在同一直线上,连接 BD.
(1)、求证:DE=CE.(2)、若∠CDE=35°,求∠A 的度数.22. 已知:如图,在△ABC、△ADE 中,∠BAC=∠DAE=90°,AB=AC,AD=AE, 点 C、D、E 三点在同一直线上,连接 BD.求证:
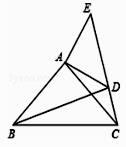 (1)、△BAD≌△CAE;(2)、试猜想 BD、CE 有何特殊位置关系,并证明
(1)、△BAD≌△CAE;(2)、试猜想 BD、CE 有何特殊位置关系,并证明
23. 中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC 中,∠ACB=90°,若 AC=b,BC=a,请你利用这个图形解决下列问题: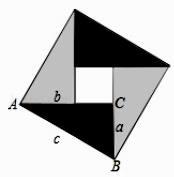 (1)、试说明 a2+b2=c2;(2)、如果大正方形的面积是 10,小正方形的面积是2,求(a+b)2的值.24. 如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.(1)、在方程①3x-1=0,② ③x-(3x+1)=-5 中,不等组 的关联方程是(2)、若不等式组 的一个关联方程的根是整数, 则这个关联方程可以是(写出一个即可)(3)、若方程 3-x=2x,3+x= 都是关于 x 的不等式组 的关联方程,直接写出 m 的取值范围.
(1)、试说明 a2+b2=c2;(2)、如果大正方形的面积是 10,小正方形的面积是2,求(a+b)2的值.24. 如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.(1)、在方程①3x-1=0,② ③x-(3x+1)=-5 中,不等组 的关联方程是(2)、若不等式组 的一个关联方程的根是整数, 则这个关联方程可以是(写出一个即可)(3)、若方程 3-x=2x,3+x= 都是关于 x 的不等式组 的关联方程,直接写出 m 的取值范围.
25. 某镇水库的可用水量为 12 000 万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)、问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)、政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少立方米水才能实现目标?(3)、某企业投入1000万元设备,每天能淡化5000立方米海水,淡化率为70%.每淡化1立方米海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/立方米的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?