浙教版七年级下册第1章 1.4平行线的性质 同步练习
试卷更新日期：2017-03-17 类型：同步测试
一、单选题
-
1. 在同一平面内，a，b，c是直线，下列说法正确的是（ ）A、若a∥b，b∥c，则a∥c B、若a⊥b，b⊥c，则a⊥c C、若a∥b，b⊥c，则a∥c D、若a∥b，b∥c，则a⊥c2. 如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角∠A是120°，第二次拐的角∠B是150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C的大小是（ ）
A、150° B、130° C、140° D、120°3. 如图，将一条两边沿互相平行的纸带按图折叠，则∠α的度数等于（ ）
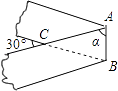A、50° B、60° C、75° D、85°4. 如图，直线a∥b，∠1=70°，那么∠2的度数是（ ）
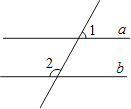A、130° B、110° C、70° D、80°5. 如图，AB∥CD，CE平分∠ACD交AB于E，若∠A=120°，则∠AEC=（ ）
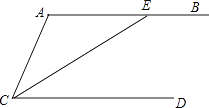A、20° B、25° C、30° D、50°6. 一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，那么两次拐弯的角度可能是（ ）A、第一次右拐15°，第二次左拐165° B、第一次左拐15°，第二次右拐15° C、第一次左拐15°，第二次左拐165° D、第一次右拐15°，第二次右拐15°7. 如图，AB∥CD，AC平分∠BCD，∠A=40°，则∠B的度数为（ ）
A、90° B、100° C、110° D、120°8. 如图，直线c与直线a、b相交，且a∥b，则结论：①∠1=∠2；②∠3+∠4=180°；③∠3=∠2；④∠1=∠4；⑤∠4+∠2=180°；⑥∠1=∠3；
其中正确的个数为（ ）
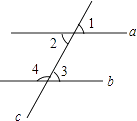A、3 B、4 C、5 D、69. 如图，AB∥CD，EF⊥AB于E，EF交CD于F，已知∠1=60°，则∠2=（ ）
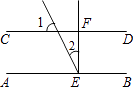A、20° B、60° C、30° D、45°10. 如图，已知AB∥CD，BC平分∠ABE，∠C=36°，则∠BED的度数是（ ）
A、18° B、36° C、58° D、72°11. 如图，已知AB∥CD，下列各角之间的关系一定成立的是（ ）
A、∠1=∠3 B、∠2=∠4 C、∠1＞∠4 D、∠3+∠5=180°12. 直线a上有一点A，直线b上有一点B，且a∥b．点P在直线a，b之间，若PA=3，PB=4，则直线a、b之间的距离（ ）A、等于7 B、小于7 C、不小于7 D、不大于713. 如图，将长方形ABCD沿线段OG折叠到OB'C'G的位置，∠OGC'等于100°，则∠DGC'的度数为（ ）
A、20° B、30° C、40° D、50°14. 如图，已知AD∥BC，∠B=30°，DB平分∠ADE，则∠DEC=（ ）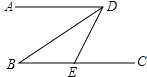
A、30° B、60° C、90° D、120°15. 如图所示，若AB∥CD，则∠A，∠D，∠E之间的度数关系是（ ）
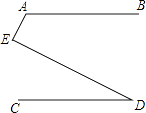A、∠A+∠E+∠D=180° B、∠A﹣∠E+∠D=180° C、∠A+∠E﹣∠D=180° D、∠A+∠E+∠D=270°二、填空题
-
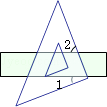
16. 如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=35°，那么∠2是度．
17. 一大门的栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD=度．
18. 用一张长方形纸条折成如图所示图形，如果∠1=130°，那么∠2= ．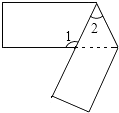
19. 如图，已知AB∥CD，BE平分∠ABC，∠CDE=150°，则∠C=°．
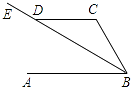20. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D，C分别在M，N的位置上，若∠EFG=56°，则∠1= ， ∠2= ．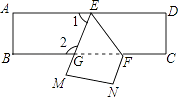
三、解答题
-
21. 如图，已知∠1=∠2，∠D=60˚，求∠B的度数．
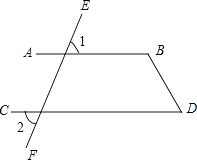22. 已知：如图，BC∥EF，AD=BE，BC=EF，试证明AC=DF．
23. 已知：如图，∠ADE=∠B，∠DEC=115°．求∠C的度数．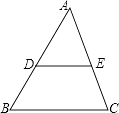
24. 如图，直线AB、CD被EF所截，∠1=∠2，∠CNF=∠BME．求证：AB∥CD，MP∥NQ．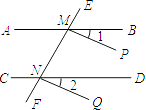
四、综合题
-
25. 如图，点D，F在线段AB上，点E，G分别在线段BC和AC上，CD∥EF，∠1=∠2．
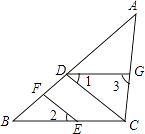(1)、判断DG与BC的位置关系，并说明理由；(2)、若DG是∠ADC的平分线，∠3=85°，且∠DCE：∠DCG=9：10，试说明AB与CD有怎样的位置关系？26. 如图，直线l1∥l2 ， 直线l与l1、l2分别交于A、B两点，点M，N分别在l1、l2上，点M，N，P均在l的同侧（点P不在l1、l2上），若∠PAM=α，∠PBN=β．
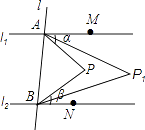(1)、当点P在l1与l2之间时．求∠APB的大小（用含α、β的代数式表示）；
(2)、若∠APM的平分线与∠PBN的平分线交于点P1 ， ∠P1AM的平分线与∠P1BN的平分线交于点P2 ， …，∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn ， 则∠AP1B= ， ∠APnB= ． （用含α、β的代数式表示，其中n为正整数）(3)、当点P不在l1与l2之间时．若∠PAM的平分线与∠PBN的平分线交于点P，∠P1AM的平分线与∠P1BN的平分线交于点P2 ， …，∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn ， 请直接写出∠APnB的大小．（用含α、β的代数式表示，其中n为正整数）
27. 平面内的两条直线有相交和平行两种位置关系
(1)、已知AB平行于CD，如a图，当点P在AB、CD外部时，∠BPD+∠D=∠B即∠BPD=∠B﹣∠D，为什么？请说明理由．如b图，将点P移动到AB、CD内部，以上结论是否仍然成立？若不成立，则∠BPD、∠B、∠D之间有何数量关系？请说明结论；(2)、在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD、∠B、∠D、∠BQD之间有何数量关系？（不需证明）(3)、根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．