2017年上海市长宁区、金山区中考数学一模试卷

试卷更新日期：2017-03-17 类型：中考模拟

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，抛物线y=﹣（x﹣1）²+2的顶点坐标是（）

A、（﹣1，2） B、（1，2） C、（2，﹣1） D、（2，1）

查看试题解析
2. 在△ABC中，∠C=90°，AB=5，BC=4，那么∠A的正弦值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
3. 如图，下列能判断BC∥ED的条件是（）

A、 $\frac{E D}{B C} = \frac{A D}{A B}$ B、 $\frac{E D}{B C} = \frac{A E}{A C}$ C、 $\frac{A D}{A B} = \frac{A E}{A C}$ D、 $\frac{A D}{A B} = \frac{A C}{A E}$

查看试题解析
4. 已知⊙O₁与⊙O₂的半径分别是2和6，若⊙O₁与⊙O₂相交，那么圆心距O₁O₂的取值范围是（）

A、2＜O₁O₂＜4 B、2＜O₁O₂＜6 C、4＜O₁O₂＜8 D、4＜O₁O₂＜10

查看试题解析
5. 已知非零向量 $\vec{a}$ 与 $\vec{b}$ ，那么下列说法正确的是（）

A、如果| $\vec{a}$ |=| $\vec{b}$ |，那么 $\vec{a}$ = $\vec{b}$ B、如果| $\vec{a}$ |=|﹣ $\vec{b}$ |，那么 $\vec{a}$ ∥ $\vec{b}$ C、如果 $\vec{a}$ ∥ $\vec{b}$ ，那么| $\vec{a}$ |=| $\vec{b}$ | D、如果 $\vec{a}$ =﹣ $\vec{b}$ ，那么| $\vec{a}$ |=| $\vec{b}$ |

查看试题解析
6. 已知等腰三角形的腰长为6cm，底边长为4cm，以等腰三角形的顶角的顶点为圆心5cm为半径画圆，那么该圆与底边的位置关系是（）

A、相离 B、相切 C、相交 D、不能确定

查看试题解析

二、填空题

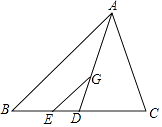
7. 如果3x=4y，那么 $\frac{x}{y}$ = ．

查看试题解析
8. 已知二次函数y=x²﹣2x+1，那么该二次函数的图象的对称轴是．

查看试题解析
9. 已知抛物线y=3x²+x+c与y轴的交点坐标是（0，﹣3），那么c= ．

查看试题解析
10. 已知抛物线y=﹣ $\frac{1}{2}$ x²﹣3x经过点（﹣2，m），那么m= ．

查看试题解析
11. 设α是锐角，如果tanα=2，那么cotα= ．

查看试题解析
12. 在直角坐标平面中，将抛物线y=2x²先向上平移1个单位，再向右平移1个单位，那么平移后的抛物线解析式是．

查看试题解析
13. 已知⊙A的半径是2，如果B是⊙A外一点，那么线段AB长度的取值范围是．

查看试题解析
14. 如图，点G是△ABC的重心，联结AG并延长交BC于点D，GE∥AB交BC与E，若AB=6，那么GE= ．

查看试题解析
15.
如图，在地面上离旗杆BC底部18米的A处，用测角仪测得旗杆顶端C的仰角为30°，已知测角仪AD的高度为1.5米，那么旗杆BC的高度为米．

查看试题解析
16. 如图，⊙O₁与⊙O₂相交于A、B两点，⊙O₁与⊙O₂的半径分别是1和 $\sqrt{3}$ ，O₁O₂=2，那么两圆公共弦AB的长为．

查看试题解析
17. 如图，在梯形ABCD中，AD∥BC，AC与BD交于O点，DO：BO=1：2，点E在CB的延长线上，如果S_△_AOD：S_△_ABE=1：3，那么BC：BE= ．

查看试题解析
18. 如图，在△ABC中，∠C=90°，AC=8，BC=6，D是AB的中点，点E在边AC上，将△ADE沿DE翻折，使得点A落在点A'处，当A'E⊥AC时，A'B= ．

查看试题解析

三、解答题

19. 计算：sin30°•tan30°﹣ $\frac{1}{3}$ cos60°•cot30°+ $\frac{\tan 45^{\circ}}{\sin^{2} 45^{\circ}}$ ．

查看试题解析
20. 如图，在△ABC中，D是AB中点，联结CD．

(1)、若AB=10且∠ACD=∠B，求AC的长．

(2)、过D点作BC的平行线交AC于点E，设 $\vec{D E}$ = $\vec{a}$ ， $\vec{D C}$ = $\vec{b}$ ，请用向量 $\vec{a}$ 、 $\vec{b}$ 表示 $\vec{A C}$ 和 $\vec{A B}$ （直接写出结果）

查看试题解析
21. 如图，△ABC中，CD⊥AB于点D，⊙D经过点B，与BC交于点E，与AB交与点F．已知tanA= $\frac{1}{2}$ ，cot∠ABC= $\frac{3}{4}$ ，AD=8．

(1)、⊙D的半径；

(2)、CE的长．

查看试题解析
22. 如图，拦水坝的横断面为梯形ABCD，AB∥CD，坝顶宽DC为6米，坝高DG为2米，迎水坡BC的坡角为30°，坝底宽AB为（8+2 $\sqrt{3}$ ）米．

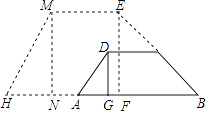(1)、求背水坡AD的坡度；

(2)、为了加固拦水坝，需将水坝加高2米，并且保持坝顶宽度不变，迎水坡和背水坡的坡度也不变，求加高后坝底HB的宽度．

查看试题解析
23. 如图，已知正方形ABCD，点E在CB的延长线上，联结AE、DE，DE与边AB交于点F，FG∥BE且与AE交于点G．

(1)、求证：GF=BF．

(2)、在BC边上取点M，使得BM=BE，联结AM交DE于点O．求证：FO•ED=OD•EF．

查看试题解析
24. 在平面直角坐标系中，抛物线y=﹣x²+2bx+c与x轴交于点A、B（点A在点B的右侧），且与y轴正半轴交于点C，已知A（2，0）

(1)、当B（﹣4，0）时，求抛物线的解析式；

(2)、O为坐标原点，抛物线的顶点为P，当tan∠OAP=3时，求此抛物线的解析式；

(3)、O为坐标原点，以A为圆心OA长为半径画⊙A，以C为圆心， $\frac{1}{2}$ OC长为半径画圆⊙C，当⊙A与⊙C外切时，求此抛物线的解析式．

查看试题解析
25.
已知△ABC，AB=AC=5，BC=8，∠PDQ的顶点D在BC边上，DP交AB边于点E，DQ交AB边于点O且交CA的延长线于点F（点F与点A不重合），设∠PDQ=∠B，BD=3．

(1)、求证：△BDE∽△CFD；

(2)、设BE=x，OA=y，求y关于x的函数关系式，并写出定义域；

(3)、当△AOF是等腰三角形时，求BE的长．

查看试题解析