2017年上海市黄浦区中考数学一模试卷

试卷更新日期：2017-03-17 类型：中考模拟

进入出卷网下载

一、一.选择题

1. 下列抛物线中，与抛物线y=x²﹣2x+4具有相同对称轴的是（）

A、y=4x²+2x+1 B、y=2x²﹣4x+1 C、y=2x²﹣x+4 D、y=x²﹣4x+2

查看试题解析
2. 如图，点D、E位于△ABC的两边上，下列条件能判定DE∥BC的是（）

A、AD•DB=AE•EC B、AD•AE=BD•EC C、AD•CE=AE•BD D、AD•BC=AB•DE

查看试题解析
3. 已知一个坡的坡比为i，坡角为α，则下列等式成立的是（）

A、i=sinα B、i=cosα C、i=tanα D、i=cotα

查看试题解析
4. 已知向量 $\vec{a}$ 和 $\vec{b}$ 都是单位向量，则下列等式成立的是（）

A、 $\vec{a} = \vec{b}$ B、 $\vec{a} + \vec{b} = 2$ C、 $\vec{a} - \vec{b} = 0$ D、| $\vec{a}$ |﹣| $\vec{b}$ |=0

查看试题解析
5. 已知二次函数y=x² ，将它的图象向左平移2个单位，再向上平移3个单位，则所得图象的表达式为（）

A、y=（x+2）²+3 B、y=（x+2）²﹣3 C、y=（x﹣2）²+3 D、y=（x﹣2）²﹣3

查看试题解析
6. Word文本中的图形，在图形格式中大小菜单下显示有图形的绝对高度和绝对宽度，同一个图形随其放置方向的变化，所显示的绝对高度和绝对宽度也随之变化．如图①、②、③是同一个三角形以三条不同的边水平放置时，它们所显示的绝对高度和绝对宽度如下表，现有△ABC，已知AB=AC，当它以底边BC水平放置时（如图④），它所显示的绝对高度和绝对宽度如下表，那么当△ABC以腰AB水平放置时（如图⑤），它所显示的绝对高度和绝对宽度分别是（）
图形
图①
图②
图③
图④
图⑤
绝对高度
1.50
2.00
1.20
2.40
？
绝对宽度
2.00
1.50
2.50
3.60
？

A、3.60和2.40 B、2.56和3.00 C、2.56和2.88 D、2.88和3.00

查看试题解析

二、二.填空题

7. 已知线段a是线段b、c的比例中项，如果a=3，b=2，那么c=

查看试题解析
8. 化简： $2 (\vec{a} - 2 \vec{b}) - 3 (\vec{a} + \vec{b})$ = ．

查看试题解析
9. 已知点P是线段AB的黄金分割点（AP＞BP），若AB=2，则AP﹣BP=

查看试题解析
10. 已知二次函数y=f（x）的图象开口向上，对称轴为直线x=4，则f（1） f（5）（填“＞”或“＜”）

查看试题解析
11. 求值：sin60°•tan30°= ．

查看试题解析
12. 已知G是等腰直角△ABC的重心，若AC=BC=2，则线段CG的长为

查看试题解析
13. 两个相似三角形的相似比为2：3，则它们的面积之比为

查看试题解析
14. 等边三角形的周长为C，面积为S，则面积S关于周长C的函数解析式为．

查看试题解析
15. 如图，正方形ABCD的边EF在△ABC的边BC上，顶点D、G分别在边AB、AC上，已知BC=6，△ABC的面积为9，则正方形DEFG的面积为

查看试题解析
16.
如图，小明家所在小区的前后两栋楼AB、CD，小明在自己所住楼AB的底部A处，利用对面楼CD墙上玻璃（与地面垂直）的反光，测得楼AB顶部B处的仰角是α，若tanα=0.45，两楼的间距为30米，则小明家所住楼AB的高度是米．

查看试题解析
17. 如图，在△ABC中，∠C=90°，AC=8，BC=6，D是边AB的中点，现有一点P位于边AC上，使得△ADP与△ABC相似，则线段AP的长为．

查看试题解析
18. 如图，菱形ABCD内两点M、N，满足MB⊥BC，MD⊥DC，NB⊥BA，ND⊥DA，若四边形BMDN的面积是菱形ABCD面积的 $\frac{1}{5}$ ，则cosA= ．

查看试题解析

三、三.解答题

19. 用配方法把二次函数y= $\frac{1}{2}$ x²﹣4x+5化为y=a（x+m）²+k的形式，再指出该函数图象的开口方向、对称轴和顶点坐标．

查看试题解析
20. 如图，在梯形ABCD中，AD∥BC，AD=3，BC=2，点E、F分别在两腰上，
且EF∥AD，AE：EB=2：1；

(1)、求线段EF的长；

(2)、设 $\vec{A B}$ = $\vec{a}$ ， $\vec{A D}$ = $\vec{b}$ ，试用 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{E C}$ ．

查看试题解析
21. 如图，在△ABC中，∠ACB=90°，AB=5，tanA= $\frac{1}{3}$ ，将△ABC沿直线l翻折，恰好使点A与点B重合，直线l分别交边AB、AC于点D、E；

(1)、求△ABC的面积；

(2)、求sin∠CBE的值．

查看试题解析
22.
如图，在坡AP的坡脚A处竖有一根电线杆AB，为固定电线杆在地面C处和坡面D处各装一根等长的引拉线BC和BD，过点D作地面MN的垂线DH，H为垂足，已知点C、A、H在一直线上，若测得AC=7米，AD=12米，坡角为30^° ，试求电线杆AB的高度；（精确到0.1米）

查看试题解析
23. 如图1，点D位于△ABC边AC上，已知AB是AD与AC的比例中项．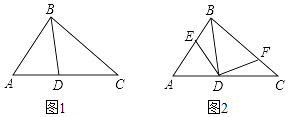

(1)、求证：∠ACB=∠ABD；

(2)、现有点E、F分别在边AB、BC上如图2，满足∠EDF=∠A+∠C，当AB=4，BC=5，CA=6时，求证：DE=DF．

查看试题解析
24.
平面直角坐标系xOy中，对称轴平行于y轴的抛物线过点A（1，0）、B（3，0）和C（4，6）；

(1)、求抛物线的表达式；

(2)、现将此抛物线先沿x轴方向向右平移6个单位，再沿y轴方向平移k个单位，若所得抛物线与x轴交于点D、E（点D在点E的左边），且使△ACD∽△AEC（顶点A、C、D依次对应顶点A、E、C），试求k的值，并注明方向．

查看试题解析
25. 如图，△ABC边AB上点D、E（不与点A、B重合），满足∠DCE=∠ABC，∠ACB=90°，AC=3，BC=4；

(1)、当CD⊥AB时，求线段BE的长；

(2)、当△CDE是等腰三角形时，求线段AD的长；

(3)、设AD=x，BE=y，求y关于x的函数解析式，并写出定义域．

查看试题解析

图形	图①	图②	图③	图④	图⑤
绝对高度	1.50	2.00	1.20	2.40	？
绝对宽度	2.00	1.50	2.50	3.60	？