2016年江西省中考大联考数学试卷(三)
试卷更新日期:2017-03-17 类型:中考模拟
一、选择题
-
1. 下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是( )A、∠A=30°,∠B=40° B、∠A=30°,∠B=110° C、∠A=30°,∠B=70° D、∠A=30°,∠B=90°2. 下列各数中是有理数的是( )A、 B、4π C、sin45° D、3. 关于函数y=2x , 下列结论中正确的是( )A、函数图象都经过点(2,1) B、函数图象都经过第二、四象限 C、y随x的增大而增大 D、不论x取何值,总有y>04. 如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )A、
 B、
B、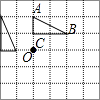 C、
C、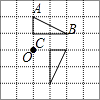 D、
D、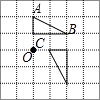 5. 如图,有一个正方体纸巾盒,它的平面展开图是( )
5. 如图,有一个正方体纸巾盒,它的平面展开图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,图1是由5个完全相同的正方体堆成的几何体,现将标有E的正方体平移至如图2所示的位置,下列说法中正确的是( )
6. 如图,图1是由5个完全相同的正方体堆成的几何体,现将标有E的正方体平移至如图2所示的位置,下列说法中正确的是( ) A、左、右两个几何体的主视图相同 B、左、右两个几何体的左视图相同 C、左、右两个几何体的俯视图不相同 D、左、右两个几何体的三视图不相同
A、左、右两个几何体的主视图相同 B、左、右两个几何体的左视图相同 C、左、右两个几何体的俯视图不相同 D、左、右两个几何体的三视图不相同二、填空题
-
7. 函数y= 中,自变量x的取值范围是 .8. 生物学家发现了一种病毒的长度约为0.00000432毫米,数据0.00000432用科学记数法表示为9. 如图是某几何体的三视图,根据图中数据,求得该几何体的体积为 .
 10. 已知﹣x2+4x的值为6,则2x2﹣8x+4的值为 .11. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有50个,除颜色外,形状、大小、质地完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在20%和40%,则布袋中白色球的个数很可能是 个.12. 如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为
10. 已知﹣x2+4x的值为6,则2x2﹣8x+4的值为 .11. 在一个不透明的布袋中,红色、黑色、白色的玻璃球共有50个,除颜色外,形状、大小、质地完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率分别稳定在20%和40%,则布袋中白色球的个数很可能是 个.12. 如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′,A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为 13.
13.如图,点A、B是反比例函数 (x>0)图象上的两个点,在△AOB中,OA=OB,BD垂直于x轴,垂足为D,且AB=2BD,则△AOB的面积为
 14. 如图,半径为1的⊙P在射线AB上运动,且A(﹣3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是
14. 如图,半径为1的⊙P在射线AB上运动,且A(﹣3,0)B(0,3),那么当⊙P与坐标轴相切时,圆心P的坐标是
三、解答题
-
15. 解不等式组: ,并在数轴上把解集表示出来.16. 已知(a+2+ )2与|b+2﹣ |互为相反数,求(a+2b)2﹣(2b+a)(2b﹣a)﹣2a2的值.17. 当a<﹣1时,代数式6﹣9a﹣ 的值是正的还是负的?试说明你的理由.18. 如图,坐标平面上,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC=5.若A点的坐标为(﹣3,1),B、C两点在直线y=﹣3上,D、E两点在y轴上.
 (1)、在△ABC中,作AH、CK分别垂直BC、AB于H、K,求证:KC=HA;(2)、求F点到y轴的距离.19.
(1)、在△ABC中,作AH、CK分别垂直BC、AB于H、K,求证:KC=HA;(2)、求F点到y轴的距离.19.如图,下列正方形网格的每个小正方形的边长均为1,⊙O的半径为n≥8 .规定:顶点既在圆上又是正方形格点的直角三角形称为“圆格三角形”,请按下列要求各画一个“圆格三角形”,并用阴影表示出来.
 20. 某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
20. 某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).表1
一班
5
8
8
9
8
10
10
8
5
5
二班
10
6
6
9
10
4
5
7
10
8
表2
班级
平均数
中位数
众数
方差
及格率
优秀率
一班
7.6
8
a
3.82
70%
30%
二班
b
7.5
10
4.94
80%
40%
(1)、在表2中,a= , b=;(2)、有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;(3)、一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.21. 4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包,已知“雀巢巧克力”每包22元,“趣多多小饼干”每包2元,总共花费了80元.(1)、请求出小欣在这次采购中,“雀巢巧克力”和“趣多多小饼干”各买了多少包?(2)、“五•一”期间,小欣发现,A、B两超市以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在A超市累计购物超过50元后,超过50元的部分打九折;在B超市累计购物超过100元后,超过100元的部分打八折.①请问“五•一”期间,若小欣购物金额超过100元,去哪家超市购物更划算?
②“五•一”期间,小欣又到“B超市”购买了一些“雀巢巧克力”,请问她至少购买多少包时,平均每包价格不超过20元?
22.如图,已知△ABD和△CEF都是斜边为2cm的全等直角三角形,其中∠ABD=∠FEC=60°,且B、D、C、E都在同一直线上,DC=4.
 (1)、求证:四边形ABFE是平行四边形.(2)、△ABD沿着BE的方向以每秒1cm的速度运动,设△ABD运动的时间为t秒,
(1)、求证:四边形ABFE是平行四边形.(2)、△ABD沿着BE的方向以每秒1cm的速度运动,设△ABD运动的时间为t秒,①当t为何值时,▱ABFE是菱形?请说明你的理由.
②▱ABFE有可能是矩形吗?若可能,求出t的值及此矩形的面积;若不可能,请说明理由.
23. 已知二次函数 .(1)、求证:不论k为任何实数,该函数的图象与x轴必有两个交点;(2)、若该二次函数的图象与x轴的两个交点在点A(1,0)的两侧,且关于x的一元二次方程k2x2+(2k+3)x+1=0有两个不相等的实数根,求k的整数值;(3)、在(2)的条件下,关于x的另一方程x2+2(a+k)x+2a﹣k2+6k﹣4=0 有大于0且小于3的实数根,求a的整数值.24. 已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题: (1)、如图①,若点P在线段AB上,且AC=1+ ,PA= ,则:
(1)、如图①,若点P在线段AB上,且AC=1+ ,PA= ,则:①线段PB= , PC=;
②猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)、如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;(3)、若动点P满足 = ,求 的值.(提示:请利用备用图进行探求)