2016年江苏省扬州市高邮市中考数学三模试卷
试卷更新日期:2017-03-17 类型:中考模拟
一、选择题
-
1. 计算﹣5+|﹣3|的结果是( )A、2 B、﹣2 C、8 D、﹣82. 某红外线遥控器发出的红外线波长为0.000 000 94m,用科学记数法表示这个数为( )A、9.4×10﹣8m B、9.4×108m C、9.4×10﹣7m D、9.4×107m3. 下列图形中,由 ,能得到 的是( )A、
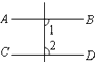 B、
B、 C、
C、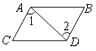 D、
D、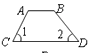 4. 如图,是把圆柱体沿上面的直径截去一部分后剩下的物体图形,它的俯视图是( )
4. 如图,是把圆柱体沿上面的直径截去一部分后剩下的物体图形,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 学校食堂午餐有10元,12元、15元三种价格的盒饭供选择,若经过统计发现10元、12元、15元的盒饭卖出数量恰好分别占50%,30%、20%,则卖出盒饭价格的中位数是( )A、10元 B、11元 C、12元 D、无法确定6. 如图,动点P从点A出发,沿半圆AB匀速运动到达终点B,若以时间t为自变量,扇形OAP的面积S为函数图象大致是( )
5. 学校食堂午餐有10元,12元、15元三种价格的盒饭供选择,若经过统计发现10元、12元、15元的盒饭卖出数量恰好分别占50%,30%、20%,则卖出盒饭价格的中位数是( )A、10元 B、11元 C、12元 D、无法确定6. 如图,动点P从点A出发,沿半圆AB匀速运动到达终点B,若以时间t为自变量,扇形OAP的面积S为函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )
7. 如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( ) A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
8. 写出绝对值小于2的一个负数: .9. 分解因式x2(x﹣2)+4(2﹣x)=10. 若等腰三角形的一个外角的度数为40°,则这个等腰三角形顶角的度数是 .11. 在Rt△ABC中,∠C=90°,点G是Rt△ABC的重心,如果CG=6,那么斜边AB的长等于 .
12. 某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示.甲
乙
丙
丁
平均数/环
9.7
9.5
9.5
9.7
方差/环2
5.1
4.7
4.5
4.5
请你根据表中数据选一人参加比赛,最合适的人选是 .
13. 如图,若用若干个全等的等腰梯形拼成了一个平行四边形,则一个等腰梯形中,最大的内角是 . 14. 如图,点C′与半圆上的点C关于直径AB成轴对称.若∠AOC=40°,则∠CC′B=°.
14. 如图,点C′与半圆上的点C关于直径AB成轴对称.若∠AOC=40°,则∠CC′B=°. 15. 如图,三个全等的小矩形沿“橫﹣竖﹣橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于 cm.
15. 如图,三个全等的小矩形沿“橫﹣竖﹣橫”排列在一个大矩形中,若这个大矩形的周长为2016cm,则一个小矩形的周长等于 cm. 16. 在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如下表:
16. 在二次函数y=﹣x2+bx+c中,函数y与自变量x的部分对应值如下表:x
﹣3
﹣2
﹣1
1
2
3
4
5
6
y
﹣14
﹣7
﹣2
2
m
n
﹣7
﹣14
﹣23
则m、n的大小关系为 mn.(填“<”,“=”或“>”)
17. 若函数y=x2﹣3|x﹣1|﹣4x﹣3﹣b(b为常数)的图象与x轴恰好有三个交点,则常数b的值为 .三、解答题
-
18. 计算:﹣32+ ﹣(cos30°﹣1)0﹣(﹣ )﹣3+82×0.1252 .19. 先化简,再求值: ÷(m﹣1﹣ ),其中m=﹣3.20. 为了解高邮市6000名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分30分,得分均为整数),制成下表:
分数段(x分)
x≤10
11≤x≤15
16≤x≤20
21≤x≤25
26≤x≤30
人 数
10
15
35
112
128
(1)、本次抽样调查共抽取了名学生;(2)、若用扇形统计图表示统计结果,则分数段为x≤10的人数所对应扇形的圆心角为°;(3)、学生英语口语考试成绩的众数落在11≤x≤15的分数段内;(填“会”或“不会”)(4)、若将26分以上(含26)定为优秀,请估计该区九年级考生成绩为优秀的人数.21. 学校为参加高邮市“五运会”广播操表演,准备从七、八、九三个年级分别选送到位的一男、一女共6名备选人中,每个年级随机选出1名学生,共3名学生担任领操员(1)、选出3名领操员中,男生的人数可能是(2)、求选出“两男一女”3名领操员的概率.22. 一家文具超市营业员的流水账记录;五月一日卖出15本笔记本和5只计算器,收入225元,五月二日以同样的价格卖出同样的3本笔记本和6只计算器,收入285元,请你用二元一次方程组的知识进行分析,这个记录是否有错误?23. 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(﹣1,0),与反比例函数y= 在第一象限内的图象交于点B( ,n).连接OB,若S△AOB=1. (1)、求反比例函数与一次函数的关系式;(2)、直接写出不等式组 的解集.24. 如图,△ABC中,AB=4,AC=2,BC=2 ,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E.
(1)、求反比例函数与一次函数的关系式;(2)、直接写出不等式组 的解集.24. 如图,△ABC中,AB=4,AC=2,BC=2 ,以BC为直径的半圆交AB于点D,以A为圆心,AC为半径的扇形交AB于点E. (1)、以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;(2)、求图中阴影部分的面积(结果可保留根号和π).25. 如图,已知在△ABC中,AB=AC,tan∠B=2,BC=4,D为BC边的中点,点E在BC边的延长线上,且CE=BC,连接AE,F为线段AE的中点
(1)、以BC为直径的圆与AC所在的直线有何位置关系?请说明理由;(2)、求图中阴影部分的面积(结果可保留根号和π).25. 如图,已知在△ABC中,AB=AC,tan∠B=2,BC=4,D为BC边的中点,点E在BC边的延长线上,且CE=BC,连接AE,F为线段AE的中点 (1)、求线段CF的长;(2)、求∠CAE的正弦值.26. 小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下“促销优惠”方案:
(1)、求线段CF的长;(2)、求∠CAE的正弦值.26. 小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下“促销优惠”方案:若一次购买数量超过10件,则每增加一件,所有这一款童装的售价降低1元/件,例如一次购买11件时,这11件的售价都为99元/件,但最低售价为80元/件,一次购买这一款童装的售价y元/件与购买量x件之间的函数关系如图.
 (1)、一次购买20件这款童装的售价为元/件;图中n的值为;(2)、设小颖妈妈的网店一次销售x件所获利润为w元,求w与x之间的函数关系式;(3)、小颖通过计算发现:卖25件可以赚625元,而卖30件只赚600元,为了保证销量越大利润就越大,在其他条件不变的情况下,求最低售价应定为多少元/件?27. 如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t.
(1)、一次购买20件这款童装的售价为元/件;图中n的值为;(2)、设小颖妈妈的网店一次销售x件所获利润为w元,求w与x之间的函数关系式;(3)、小颖通过计算发现:卖25件可以赚625元,而卖30件只赚600元,为了保证销量越大利润就越大,在其他条件不变的情况下,求最低售价应定为多少元/件?27. 如图,已知矩形ABCD中,AB=4cm,BC=6cm,动点P从点C开始,以1cm/s的速度在BC的延长线上向右匀速运动,连接AP交CD边于点E,把射线AP沿直线AD翻折,交CD的延长线于点Q,设点P的运动时间为t. (1)、若DQ=3cm,求t的值;(2)、设DQ=y,求出y与t的函数关系式;(3)、当t为何值时,△CPE与△AEQ的面积相等?(4)、在动点P运动过程中,△APQ的面积是否会发生变化?若变化,求出△APQ的面积S关于t的函数关系式;若不变,说明理由,并求出S的定值.
(1)、若DQ=3cm,求t的值;(2)、设DQ=y,求出y与t的函数关系式;(3)、当t为何值时,△CPE与△AEQ的面积相等?(4)、在动点P运动过程中,△APQ的面积是否会发生变化?若变化,求出△APQ的面积S关于t的函数关系式;若不变,说明理由,并求出S的定值.