2016年湖南省张家界市中考数学模拟试卷（三）

试卷更新日期：2017-03-17 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的相反数的倒数是（）

A、- $\frac{1}{2}$ B、 $\frac{1}{2}$ C、﹣2 D、2

查看试题解析
2. 下列计算正确的是（　　）

A、a²•a³=a⁶ B、（x³）²=x⁶ C、3m+2n=5mn D、y³•y³=y

查看试题解析
3. 在坐标平面内，若点P（x﹣2，x+1）在第二象限，则x的取值范围是（）

A、x＞2 B、x＜2 C、x＞﹣1 D、﹣1＜x＜2

查看试题解析
4. 一个不透明的口袋中装有3个红球和12个黄球，这些球除了颜色外，无其他差别，从中随机摸出一个球，恰好是红球的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $\frac{1}{5}$ D、 $\frac{4}{5}$

查看试题解析
5.
如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上一个动点，若PA=3，则PQ的最小值为（　　）

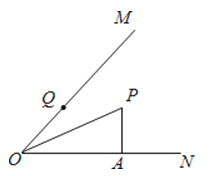A、 $\sqrt{3}$ B、2 C、3 D、2 $\sqrt{3}$

查看试题解析
6. 如图，AB为⊙O的直径，CD为⊙O的弦，∠ABD=53°，则∠BCD为（）

A、37° B、47° C、45° D、53°

查看试题解析
7. 如图是某个几何体的三视图，该几何体是（）

A、长方体 B、正方体 C、圆柱 D、三棱柱

查看试题解析
8. 抛物线y=ax²+bx+c图象如图所示，则一次函数y=﹣bx﹣4ac+b²与反比例函数y= $\frac{a + b + c}{x}$ 在同一坐标系内的图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 温家宝总理强调，“十二五”期间，将新建保障性住房36000000套，用于解决中低收入和新参加工作的大学生住房的需求．把36000000用科学记数法表示应是．

查看试题解析
10. 在函数y= $\frac{\sqrt{x + 1}}{x}$ 中，自变量x的取值范围是．

查看试题解析
11. 已知扇形的圆心角为45°，半径长为12，则该扇形的弧长为．

查看试题解析
12. 如图，这是一个长方体的主视图和俯视图，由图示数据（单元：cm）可以得出该长方体的体积是cm³ ．

查看试题解析
13. 如图，AB是⊙O的弦，OC⊥AB于点C，若AB=8cm，OC=3cm，则⊙O的半径为 cm．

查看试题解析
14. 如图，n个边长为1的相邻正方形的一边均在同一直线上，点M₁ ， M₂ ， M₃ ， …M_n分别为边B₁B₂ ， B₂B₃ ， B₃B₄ ， …，B_nB_n₊₁的中点，△B₁C₁M₁的面积为S₁ ， △B₂C₂M₂的面积为S₂ ， …△B_nC_nM_n的面积为S_n ，则S_n= ．（用含n的式子表示）

查看试题解析

三、解答题

15. 计算：（﹣2016）⁰+| $\sqrt{3}$ ﹣2|+（ $\frac{1}{2}$ ）^﹣²+3tan30°．

查看试题解析
16. $\frac{x + 1}{x}$ ÷（x﹣ $\frac{1 + x^{2}}{2 x}$ ），再从1、0、 $\sqrt{2}$ 中选一个你所喜欢的数代入求值．

查看试题解析
17. 某园林队计划由6名工人对180平方米的区域进行绿化，由于施工时增加了2名工人，结果比计划提前3小时完成任务．若每人每小时绿化面积相同，求每人每小时的绿化面积．

查看试题解析
18.
某小学三年级到六年级的全体学生参加“礼仪”知识测试，试题共有10题，每题10分．从中随机抽取了部分学生的成绩进行统计，发现抽测的学生每人至少答对了6题，现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”．

                   成绩情况统计表
成绩
100分
90分
80分
70分
60分
人数
21
40


5
频率


0.3


根据图表中提供的信息，回答下列问题：

(1)、请将统计表补充完整
                               成绩情况统计表
成绩
100分
90分
80分
70分
60分
人数
21
40

5
频率

0.3

(2)、测试学生中，成绩为80分的学生人数有名；众数是分；中位数是分；

(3)、若该小学三年级到六年级共有1800名学生，则可估计出成绩为70分的学生人数约有名．

查看试题解析
19.
如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为
A（﹣1，1），B（﹣3，1），C（﹣1，4）．

(1)、画出△ABC关于y轴对称的△A₁B₁C₁；

(2)、将△ABC绕着点B顺时针旋转90°后得到△A₂BC₂ ，请在图中画出△A₂BC₂ ，并求出线段BC旋转过程中所扫过的面积（结果保留π）．

查看试题解析
20.
如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2m，台阶AC的倾斜角∠ACB为30°，且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽略不计）．

查看试题解析
21. 如图，四边形ABCD是矩形，点E在BC边上，点F在BC延长线上，且∠CDF=∠BAE．

(1)、求证：四边形AEFD是平行四边形；

(2)、若DF=3，DE=4，AD=5，求CD的长度．

查看试题解析
22. 如图，已知AB是⊙O的直径，直线CD与⊙O相切于C点，AC平分∠DAB．

(1)、求证：AD⊥CD；

(2)、若AD=2， $A C = \sqrt{6}$ ，求⊙O的半径R的长．

查看试题解析
23. 使得函数值为零的自变量的值称为函数的零点．例如，对于函数y=x﹣1，令y=0，可得x=1，我们就说1是函数y=x﹣1的零点．已知y=x²+kx﹣4（k为常数）．

(1)、当k=0时，求该函数的零点；

(2)、证明：无论k取何值，该函数总有两个零点．

查看试题解析
24.
已知抛物线y=﹣x²+bx+c的图象经过点A（m，0）、B（0，n），其中m、n是方程x²﹣6x+5=0的两个实数根，且m＜n．

(1)、求抛物线的解析式；

(2)、设（1）中的抛物线与x轴的另一个交点为C，抛物线的顶点为D，求C、D点的坐标和△BCD的面积；

(3)、P是线段OC上一点，过点P作PH⊥x轴，交抛物线于点H，若直线BC把△PCH分成面积相等的两部分，求P点的坐标．

查看试题解析

成绩	100分	90分	80分	70分	60分
人数	21	40			5
频率			0.3

成绩	100分	90分	80分	70分	60分
人数	21	40			5
频率			0.3