2016年湖南省娄底市新化县中考数学三模试卷

试卷更新日期：2017-03-17 类型：中考模拟

进入出卷网下载

一、选择题

1. 如果a与﹣3互为相反数，那么a等于（　　）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、- $\frac{1}{3}$

查看试题解析
2. 南海是我国固有领海，它的面积超过东海、黄海、渤海面积的总和，约为360万平方千米，360万用科学记数法表示为（）

A、3.6×10² B、360×10⁴ C、3.6×10⁴ D、3.6×10⁶

查看试题解析
3. 2016年是中国农历丙申猴年，下列四个猴子头像中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 不等式3（x﹣1）+4≥2x的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
5. 将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为（）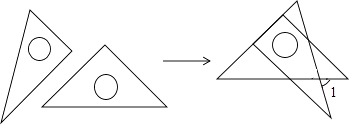

A、75° B、60° C、45° D、30°

查看试题解析
6.
如图，在平行四边形ABCD中，点E是边AD上一点，且AE=2ED，EC交对角线BD于点F，则 $\frac{E F}{F C}$ 等于（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
7. 如图，在菱形ABCD中，对角线AC，BD相交于点O，点E为BC的中点，则下列等式中一定成立的是（）

A、AB=BE B、AC=2AB C、AB=2OE D、AC=2OE

查看试题解析
8. 对于非零实数a、b，规定a⊗b= $\frac{1}{b} - \frac{1}{a}$ ．若2⊗（2x﹣1）=1，则x的值为（）

A、 $\frac{5}{6}$ B、 $\frac{5}{4}$ C、 $\frac{3}{2}$ D、﹣ $\frac{1}{6}$

查看试题解析
9. 济南某中学足球队的18名队员的年龄如表所示：
年龄（单位：岁）
12
13
14
15
人数
3
5
6
4
这18名队员年龄的众数和中位数分别是（）

A、13岁，14岁 B、14岁，14岁 C、14岁，13岁 D、14岁，15岁

查看试题解析
10. 如图，A，B，C，D为⊙O的四等分点，动点P从圆心O出发，沿O﹣C﹣D﹣O路线作匀速运动，设运动时间为t（s）．∠APB=y（°），则下列图象中表示y与t之间函数关系最恰当的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 已知m+n=3，m﹣n=2，那么m²﹣n²的值是．

查看试题解析
12. 如图，若在象棋棋盘上建立直角坐标系，使“帅”位于点（﹣3，﹣2），“炮”位于点（﹣2，0），则“兵”位于的点的坐标为

查看试题解析
13. 已知函数满足下列两个条件：
①x＞0时，y随x的增大而增大；
②它的图象经过点（1，2）．
请写出一个符合上述条件的函数的表达式

查看试题解析
14. 如图，⊙O的半径为5，正五边形ABCDE内接于⊙O，则 $\hat{A B}$ 的长度为．

查看试题解析
15. 如图，分别过等边△ABC的顶点A、B作直线a，b，使a∥b．若∠1=40°，则∠2的度数为．

查看试题解析
16. 已知一元二次方程x²﹣6x﹣5=0的两根为a、b，则 $\frac{1}{a} + \frac{1}{b}$ 的值是．

查看试题解析
17. 小张抛一枚质地均匀的硬币，出现正面朝上的可能性是．

查看试题解析
18.
观察下列图形，它们是按一定规律排列的，依照此规律，第6个图形有个太阳．

查看试题解析

三、解答题

19. 计算： $\sqrt{2}$ ﹣2sin45°﹣（1+ $\sqrt{8}$ ）⁰+2^﹣¹ ．

查看试题解析
20. 先化简，再求值：（ $\frac{1}{x - 3}$ ﹣ $\frac{x + 1}{x^{2} - 1}$ ）•（x﹣3），从不大于4的正整数中，选择一个合适的值代入x求值．

查看试题解析
21. 中学生上学带手机的现象越来越受到社会的关注，为此媒体记者随机调查了某校若干名学生上学带手机的目的，分为四种类型：A接听电话；B收发短信；C查阅资料；D游戏聊天．并将调查结果绘制成图1和图2的统计图（不完整），请根据图中提供的信息，解答下列问题：

(1)、此次抽样调查中，共调查了名学生；

(2)、将图1、图2补充完整；

(3)、现有4名学生，其中A类两名，B类两名，从中任选2名学生，求这两名学生为同一类型的概率（用列表法或树状图法）．

查看试题解析
22.
数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度．如图，老师测得升旗台前斜坡FC的坡比为i_FC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α．已知tanα= $\frac{3}{7}$ ，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．

查看试题解析
23. 资江风光带绿化提质改造工程正如火如荼地进行，某施工队计划购买甲乙两种树苗共400棵对某段道路进行绿化改造，已知甲种树苗每棵200元，乙种树苗每棵300元．

(1)、若购买两种树苗的总金额为90000元，求需购买甲、乙两种树苗各多少棵？

(2)、若购买甲种树苗的金额不少于购买乙种树苗的金额，至少应购买甲种树苗多少棵？

查看试题解析
24. 如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．

(1)、求证：△AOE≌△COD；

(2)、若∠OCD=30°，AB= $\sqrt{3}$ ，求△AOC的面积．

查看试题解析
25. 如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D．

(1)、判断直线BC与⊙O的位置关系，并说明理由；

(2)、若AC=3，∠B=30°．
①求⊙O的半径；
②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）

查看试题解析
26.
如图，对称轴为直线x= $\frac{7}{2}$ 的抛物线经过点A（6，0）和B（0，4）．

(1)、求抛物线解析式及顶点坐标；

(2)、设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；
①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？
②是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．

查看试题解析

年龄（单位：岁）	12	13	14	15
人数	3	5	6	4