2017年内蒙古包头市十校联考高考数学模拟试卷（理科）

试卷更新日期：2017-03-16 类型：高考模拟

进入出卷网下载

一、选择题：

1. 已知集合M={x|x²＞1}，N={﹣2，﹣1，0，1，2}，则M∩N=（）

A、{0} B、{2} C、{﹣2，﹣1，1，2} D、{﹣2，2}

查看试题解析
2. 复数 $\frac{2 - i}{1 - i}$ =（）

A、 $\frac{3}{2} - \frac{i}{2}$ B、 $\frac{3}{2} + \frac{i}{2}$ C、 $- \frac{3}{2} + \frac{i}{2}$ D、 $- \frac{3}{2} - \frac{i}{2}$

查看试题解析
3.
在某中学举行的环保知识竞赛中，将三个年级参赛的学生的成绩进行整理后分为5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、第五小组，已知第二小组的频数是40，则成绩在80～100分的学生人数是（）

A、15 B、18 C、20 D、25

查看试题解析
4.
如图，某几何体的正视图、侧视图和俯视图分别是等边三角形、等腰三角形和菱形，则该几何体的体积为（）

A、3 B、4 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
5. 已知平面向量a，b的夹角为 $60^{\circ} ， a = (\sqrt{3} ， 1) ， | b | = 1$ 则 $| a + 2 b |$ =（）

A、2 B、 $\sqrt{7}$ C、2 $\sqrt{7}$ D、2 $\sqrt{3}$

查看试题解析
6. 若满足x，y约束条件 ${\begin{matrix} x - y + 1 \leq 0 \\ x - 2 y \leq 0 \\ x + 2 y - 2 \leq 0 \end{matrix}$ ，则z=x+y的最大值为（）

A、 $\frac{3}{2}$ B、1 C、﹣1 D、﹣3

查看试题解析
7.
在如图所示的程序图中，若函数f（x）= ${\begin{matrix} 2^{x} ， α_{x} \leq 0 \\ \log_{\frac{1}{2}} x ， x > 0 \end{matrix}$ ，则输出的结果是（）

A、﹣3 B、 $\frac{1}{16}$ C、 $\frac{1}{4}$ D、4

查看试题解析
8. 双曲线x²﹣ $\frac{y^{2}}{b^{2}}$ =1的左右焦点分别为F₁ ， F₂ ， P为右支上一点，且| $\vec{P F_{1}}$ |=8， $\vec{P F_{1}}$ • $\vec{P F_{2}}$ =0，则双曲线的离心率为（）

A、3 B、5 C、 $\sqrt{26}$ D、 $\frac{5}{4}$

查看试题解析
9.
在正方体ABCD﹣A₁B₁C₁D₁中，点P在线段AD₁上运动，则异面直线CP与BA₁所成的角θ的取值范围是（）

A、0＜θ＜ $\frac{π}{2}$ B、0＜θ≤ $\frac{π}{2}$ C、0≤θ≤ $\frac{π}{3}$ D、0＜θ≤ $\frac{π}{3}$

查看试题解析
10. 已知函数F（x）=xf（x），f（x）满足f（x）=f（﹣x），且当x∈（﹣∞，0]时，F'（x）＜0成立，若 $a = 2^{0.1} \cdot f (2^{0.1}) ， b = \ln 2 \cdot f (\ln 2) ， c = \log_{2} \frac{1}{8} \cdot f (\log_{2} \frac{1}{8})$ ，则a，b，c的大小关系是（）

A、a＞b＞c B、c＞a＞b C、c＞b＞a D、a＞c＞b

查看试题解析
11. 已知各项均为正数的等比数列{a_n}满足a₇=a₆+2a₅ ，若存在两项a_m ， a_n使得 $\sqrt{a_{m} a_{n}}$ =4a₁ ，则 $\frac{1}{m}$ + $\frac{4}{n}$ 的最小值为（）

A、 $\frac{3}{2}$ B、 $\frac{5}{3}$ C、 $\frac{9}{4}$ D、 $\frac{25}{6}$

查看试题解析
12. 在平面直角坐标系xOy中，直线l：y=2x﹣4，圆C的半径为1，圆心在直线l上，若圆C上存在点M，且M在圆D：x²+（y+1）²=4上，则圆心C的横坐标a的取值范围是（）

A、 $[\frac{3}{5} ， 2]$ B、 $[0 ， \frac{12}{5}]$ C、 $[2 - \frac{2}{5} \sqrt{5} ， 2 + \frac{2}{5} \sqrt{5}]$ D、 $[0 ， 2 - \frac{2}{5} \sqrt{5}] \cup [2 + \frac{2}{5} \sqrt{5} ， 4]$

查看试题解析

二、填空题

13. 已知 $\cos (\frac{π}{6} - α) = \frac{\sqrt{3}}{3}$ ，则 $\sin (\frac{π}{3} + α)$ = ．

查看试题解析
14. 在（1+x）（2+x）⁵的展开式中，x³的系数为（用数字作答）．

查看试题解析
15. 设函数f（x）=x³﹣3x+1，x∈[﹣2，2]的最大值为M，最小值为m，则M+m= ．

查看试题解析
16. 设S_n是数列{a_n}的前n项和，且 $a_{1} = - 1 ， \frac{a_{n + 1}}{S_{n + 1}} = S_{n}$ ，则S_n= ．

查看试题解析

三、解答题

17. 在△ABC中，角A，B，C对的边分别为a，b，c，且c=2，C=60°．

(1)、求 $\frac{a + b}{\sin A + \sin B}$ 的值；

(2)、若a+b=ab，求△ABC的面积S_△_ABC ．

查看试题解析
18.
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB= $\frac{1}{2}$ PD．

(1)、证明：平面PQC⊥平面DCQ；

(2)、求二面角Q﹣BP﹣C的正弦值．

查看试题解析
19. 2016年1月1日起全国统一实施全面的两孩政策．为了解适龄民众对放开生育二胎政策的态度，某市选取70后80后作为调查对象，随机调查了100人并对调查结果进行统计，70后不打算生二胎的占全部调查人数的15%，80后打算生二胎的占全部被调查人数的45%，100人中共有75人打算生二胎．

(1)、根据调查数据，判断是否有90%以上把握认为“生二胎与年龄有关”，并说明理由；

(2)、以这100人的样本数据估计该市的总体数据，且以频率估计概率，若从该市70后公民中（人数很多）随机抽取3位，记其中打算生二胎的人数为X，求随机变量X的分布列，数学期望E（X）和方差D（X）．
参考公式：
P（K²≥k）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
（ $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中n=a+b+c+d）

查看试题解析
20. 已知F₁、F₂分别是椭圆C： $\frac{x^{2}}{4}$ +y²=1的左、右焦点．

(1)、若P是第一象限内该椭圆上的一点， $\vec{P F_{1}}$ • $\vec{P F_{2}}$ =﹣ $\frac{5}{4}$ ，求点P的坐标；

(2)、设过定点M（0，2）的直线l与椭圆交于不同的两点A，B，且∠AOB为锐角（其中O为坐标原点），求直线l的斜率k的取值范围．

查看试题解析
21. 已知函数f（x）=a（x+ $\frac{b}{x}$ ）+blnx（其中a，b∈R）

（Ⅰ）当b=﹣4时，若f（x）在其定义域内为单调函数，求a的取值范围；
（Ⅱ）当a=﹣1时，是否存在实数b，使得当x∈[e，e²]时，不等式f（x）＞0恒成立，如果存在，求b的取值范围，如果不存在，说明理由（其中e是自然对数的底数，e=2.71828…）．

查看试题解析
22.
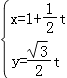已知直线l：（t为参数），曲线C₁：（θ为参数）．

（Ⅰ）设l与C₁相交于A，B两点，求|AB|；
（Ⅱ）若把曲线C₁上各点的横坐标压缩为原来的 $\frac{1}{2}$ 倍，纵坐标压缩为原来的 $\frac{\sqrt{3}}{2}$ 倍，得到曲线C₂ ，设点P是曲线C₂上的一个动点，求它到直线l的距离的最小值．

查看试题解析
23. 已知函数f（x）=|x﹣1|+|x﹣a|．

(1)、若a≤2，解不等式f（x）≥2；

(2)、若a＞1，∀x∈R，f（x）+|x﹣1|≥1，求实数a的取值范围．

查看试题解析

P（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828