广东省珠海市香洲区2018届数学中考模拟试卷（4月）
试卷更新日期：2018-11-02 类型：中考模拟
一、单选题
-
1. ﹣2018的相反数是（ ）
A、﹣2018 B、2018 C、±2018 D、2. 新建成的港珠澳大桥主体工程“海中桥隧”全长约35578米，用科学记数法表示应为（ ）A、35.578×103 B、3.5578×104 C、3.5578×105 D、0.35578×1053. 下列图形中，既是中心对称图形又是轴对称图形的是（ ）
A、正五边形 B、平行四边形 C、矩形 D、等边三角形4. 一组数据：3，2，5，3，7，5，x，它们的众数为5，则这组数据的中位数是（ ）A、2 B、3 C、5 D、75. 如图所示，已知∠AOC=∠BOD=70°，∠BOC=30°，则∠AOD的度数为（ ）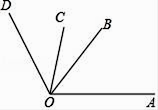
A、100° B、110° C、130° D、140°6. 下列计算正确的是（ ）A、（a2）3=a6 B、a2•a3=a6 C、a3+a4=a7 D、（ab）3=ab37. 已知一元二次方程ax2+ax﹣4=0有一个根是﹣2，则a值是（ ）A、﹣2 B、 C、2 D、48. 如图所示是8个完全相同的小正方体组成的几何体，则该几何体的左视图是（ ）
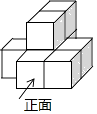A、
B、
C、
D、
9. 平面直角坐标系中，若点A（a，﹣b）在第三象限内，则点B（b，a）所在的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图，在平行四边形ABCD中，∠ABC的平分线BF交AD于点F，FE∥AB．若AB=5，AD=7，BF=6，则四边形ABEF的面积为（ ）
A、48 B、35 C、30 D、24二、填空题
-
11. 分解因式：4x2﹣36= ．12. 一个n边形的每个内角都为144°，则边数n为.
13. 若2x+y=2，则4x+1+2y的值是 ．14. 不等式组 的解集是 ．15. 如图，在⊙O中，直径AB⊥弦CD，∠A=28°，则∠D= ．
16. 如图，Rt△ABC的直角边BC在x轴上，直线y= x﹣ 经过直角顶点B，且平分△ABC的面积，BC=3，点A在反比例函数y= 图象上，则k= ．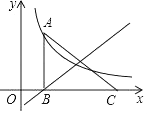
三、解答题
-
17. 计算：3﹣1﹣（2018﹣π）0+ ﹣|﹣2|．
18. 先化简，再求值： ，其中x=4．
19. 如图，正方形ABCD中，BD为对角线．
(1)、尺规作图：作CD边的垂直平分线EF，交CD于点E，交BD于点F（保留作图痕迹，不要求写作法）；
(2)、在（1）的条件下，若AB=4，求△DEF的周长．
20. 珠海某企业接到加工“无人船”某零件5000个的任务．在加工完500个后，改进了技术，每天加工的零件数量是原来的1.5倍，整个加工过程共用了35天完成．求技术改进后每天加工零件的数量．
21. 为响应香洲区全面推进书香校园建设的号召，班长小青随机调查了若干同学一周课外阅读的时间t（单位：小时），将获得的数据分成四组，绘制了如下统计图（A：0＜t≤7，B：7＜t≤14，C：14＜t≤21，D：t＞21），根据图中信息，解答下列问题：
(1)、这项工作中被调查的总人数是多少？(2)、补全条形统计图，并求出表示A组的扇形统计图的圆心角的度数；(3)、如果小青想从D组的甲、乙、丙、丁四人中先后随机选择两人做读书心得发言代表，请用列表或树状图的方法求出恰好选中甲的概率．
22. 如图1，在矩形ABCD中，AD=4，AB=2 ，将矩形ABCD绕点A逆时针旋转α（0＜α＜90°）得到矩形AEFG．延长CB与EF交于点H．
(1)、求证：BH=EH；(2)、如图2，当点G落在线段BC上时，求点B经过的路径长．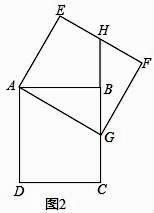
23. 如图，在平面直角坐标系中，直线y=x+2与坐标轴交于A、B两点，点A在x轴上，点B在y轴上，C点的坐标为（1，0），抛物线y=ax2+bx+c经过点A、B、C．
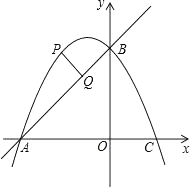(1)、求该抛物线的解析式；(2)、根据图象直接写出不等式ax2+（b﹣1）x+c＞2的解集；
(3)、点P是抛物线上一动点，且在直线AB上方，过点P作AB的垂线段，垂足为Q点．当PQ= 时，求P点坐标．24. 如图，四边形ABCD的顶点在⊙O上，BD是⊙O的直径，延长CD、BA 交于点E，连接AC、BD交于点F，作AH⊥CE，垂足为点H，已知∠ADE=∠ACB．
(1)、求证：AH是⊙O的切线；(2)、若OB=4，AC=6，求sin∠ACB的值；(3)、若 ，求证：CD=DH．25. 如图，在平面直角坐标系中，矩形OABC的顶点B坐标为（4，6），点P为线段OA上一动点（与点O、A不重合），连接CP，过点P作PE⊥CP交AB于点D，且PE=PC，过点P作PF⊥OP且PF=PO（点F在第一象限），连结FD、BE、BF，设OP=t．
(1)、直接写出点E的坐标（用含t的代数式表示）：；(2)、四边形BFDE的面积记为S，当t为何值时，S有最小值，并求出最小值；(3)、△BDF能否是等腰直角三角形，若能，求出t；若不能，说明理由．