广东省深圳市龙岗区2018届九年级数学中考一模试卷

试卷更新日期：2018-11-02 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2$ 的倒数是 $($ )

A、2 B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 在圆锥、圆柱、球当中，主视图、左视图、俯视图完全相同的有 $($ )

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 2017年龙岗区GDP总量实现历史性突破，生产总值达386000000000元，首次跃居全市各区第二 $.$ 将3860000000000用科学记数法表示为 $($ )

A、 $3.86 \times 10^{10}$ B、 $3.86 \times 10^{11}$ C、 $3.86 \times 10^{12}$ D、 $386 \times 10^{9}$

查看试题解析
4. 观察下列图形，其中既是轴对称又是中心对称图形的是 $($ )

A、 B、 C、 D、

查看试题解析
5. 下列计算正确的是 $($ )

A、 $x^{2} \cdot x^{3} = x^{6}$ B、 ${(x y)}^{2} = x y^{2}$ C、 ${(x^{2})}^{4} = x^{8}$ D、 $x^{2} + x^{3} = x^{5}$

查看试题解析
6. 在 $Rt △ ABC$ 中， $∠ C = 90^{\circ}$ ，如果 $sinA = \frac{1}{3}$ ，那么 $sinB$ 的值是 $($ )

A、 $\frac{2 \sqrt{2}}{3}$ B、 $2 \sqrt{2}$ C、 $\frac{\sqrt{2}}{4}$ D、3

查看试题解析
7. 如图：能判断 $A B / / C D$ 的条件是 $($ )

A、 $∠ A = ∠ A C D$ B、 $∠ A = ∠ D C E$ C、 $∠ B = ∠ A C B$ D、 $∠ B = ∠ A C D$

查看试题解析
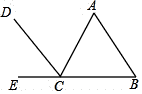8. 下列事件中，属于必然事件的是 $($ )

A、三角形的外心到三边的距离相等 B、某射击运动员射击一次，命中靶心 C、任意画一个三角形，其内角和是 $180^{\circ}$ D、抛一枚硬币，落地后正面朝上

查看试题解析
9. 一元二次方程 $x^{2} - 5 x - 6 = 0$ 的根是（）

A、 $x_{1} = 1$ ， $x_{2} = 6$ B、 $x_{1} = 2$ ， $x_{2} = 3$ C、 $x_{1} = 1$ ， $x_{2} = - 6$ D、 $x_{1} = - 1$ ， $x_{2} = 6$

查看试题解析
10. 抛物线 $y = 2 {(x + 1)}^{2} - 2$ 与 $y$ 轴的交点的坐标是（）

A、 $(0 ， - 2)$ B、 $(- 2 ， 0)$ C、 $(0 ， - 1)$ D、 $(0 ， 0)$

查看试题解析
11. 如图，菱形ABCD的周长为48cm，对角线AC、BD相交于O点，E是AD的中点，连接OE，则线段OE的长等于（）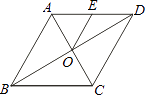

A、4cm B、5cm C、6cm D、8cm

查看试题解析
12. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图，下列四个结论：
$① 4 a + c < 0$ ； $② m (a m + b) + b > a (m \neq - 1)$ ； $③$ 关于x的一元二次方程 $a x^{2} + (b - 1) x + c = 0$ 没有实数根； $④ a k^{4} + b k^{2} < a {(k^{2} + 1)}^{2} + b (k^{2} + 1) (k$ 为常数 $)$ ．其中正确结论的个数是 $($ )

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 已知 $\frac{x}{y} = \frac{3}{2}$ ，则 $\frac{x - y}{x + y}$ = ．

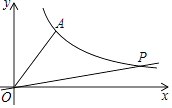
查看试题解析
14. 在实数范围内定义一种运算“*”，其规则为 $a * b = a^{2} - 2 a b + b^{2}$ ，根据这个规则求方程 $(x - 4) * 1 = 0$ 的解为．

查看试题解析
15. 将一次函数 $y = 2 x + 4$ 的图象向下平移3个单位长度，相应的函数表达式为．

查看试题解析
16. 如图，已知反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点 $A (3 ， 4)$ ，在该图象上找一点P，使 $∠ P O A = 45^{\circ}$ ，则点P的坐标为．

查看试题解析

三、解答题

17. 如图， $⊙ O$ 的半径 $O A = 2$ ，AB是弦，直线EF经过点B， $A C ⊥ E F$ 于点C， $∠ B A C = ∠ O A B$ ．

(1)、求证：EF是 $⊙ O$ 的切线；

(2)、若 $A C = 1$ ，求AB的长；

(3)、在 $(2)$ 的条件下，求图中阴影部分的面积．

查看试题解析
18. 计算： $\sqrt{27} - {(- 2)}^{0} + | 1 - \sqrt{3} | + 2 cos 30^{\circ}$ ．

查看试题解析
19. 先化简，再求值： $(\frac{a^{2}}{a - 2} - \frac{4}{a - 2}) \cdot \frac{1}{a^{2} + 2 a}$ ，其中 $a = 2 \sqrt{2}$ ．

查看试题解析
20. 当前，“精准扶贫”工作已进入攻坚阶段，凡贫困家庭均要“建档立卡” $.$ 某初级中学七年级共有四个班，已“建档立卡”的贫困家庭的学生人数按一、二、三、四班分别记为 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $A_{4}$ ，现对 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $A_{4}$ 统计后，制成如图所示的统计图．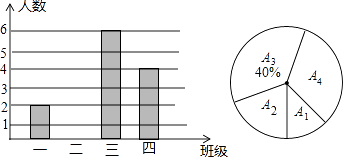

(1)、求七年级已“建档立卡”的贫困家庭的学生总人数；

(2)、将条形统计图补充完整，并求出 $A_{1}$ 所在扇形的圆心角的度数；

(3)、现从 $A_{1}$ ， $A_{2}$ 中各选出一人进行座谈，若 $A_{1}$ 中有一名女生， $A_{2}$ 中有两名女生，请用树状图表示所有可能情况，并求出恰好选出一名男生和一名女生的概率．

查看试题解析
21. 六 $\cdot$ 一前夕，某幼儿园园长到厂家选购A、B两种品牌的儿童服装，每套A品牌服装进价比B品牌服装每套进价多25元，用2000元购进A种服装数量是用750元购进B种服装数量的2倍．

(1)、求A、B两种品牌服装每套进价分别为多少元？

(2)、该服装A品牌每套售价为130元，B品牌每套售价为95元，服装店老板决定，购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套，两种服装全部售出后，可使总的获利超过1200元，则最少购进A品牌的服装多少套？

查看试题解析
22. 2014年3月，某海域发生航班失联事件，我海事救援部门用高频海洋探测仪进行海上搜救，分别在A、B两个探测点探测到C处是信号发射点，已知A、B两点相距400m，探测线与海平面的夹角分别是 $30^{\circ}$ 和 $60^{\circ}$ ，若CD的长是点C到海平面的最短距离．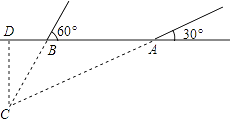

(1)、问BD与AB有什么数量关系，试说明理由；

(2)、求信号发射点的深度 $. ($ 结果精确到1m，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732)$

查看试题解析
23. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} - 3 a x - 4 a$ 的图象经过点 $C (0 ， 2)$ ，交x轴于点A、 $B (A$ 点在B点左侧 $)$ ，顶点为D．

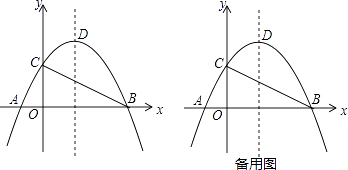(1)、求抛物线的解析式及点A、B的坐标；

(2)、将 $△ A B C$ 沿直线BC对折，点A的对称点为 $A'$ ，试求 $A'$ 的坐标；

(3)、抛物线的对称轴上是否存在点P，使 $∠ B P C = ∠ B A C$ ？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析