广东省深圳市2018届九年级中考考前押题试卷数学试卷
试卷更新日期:2018-11-02 类型:中考模拟
一、单选题
-
1. 下列计算,正确的是( )A、a5+a5=a10 B、a3÷a﹣1=a2 C、a•2a2=2a4 D、(﹣a2)3=﹣a62. 绿水青山就是金山银山,为了创造良好的生态生活环境,深圳市2017年清理河湖库塘淤泥约 方,数字用科学记数法可以表示为( )A、1.16×109 B、1.16×108 C、0. 116×109 D、11.6×1073. 抛掷一枚质地均匀的立方体骰子一次,骰子的六个面上分别标有数字1,2,3,4,5,6,则朝上一面的数字为2的概率是( )
A、 B、 C、 D、4. 实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是( )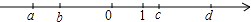 A、|a|>|b| B、|ac|=ac C、b<d D、c+d>05. 如图,直线l是一次函数y=kx+b的图象,若点A(3,m)在直线l上,则m的值是( )
A、|a|>|b| B、|ac|=ac C、b<d D、c+d>05. 如图,直线l是一次函数y=kx+b的图象,若点A(3,m)在直线l上,则m的值是( )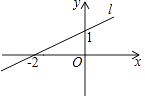 A、﹣5 B、 C、 D、76. 在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A、﹣5 B、 C、 D、76. 在平面直角坐标系中,将点A(﹣1,﹣2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
A、(﹣3,﹣2) B、(2,2) C、(﹣2,2) D、(2,﹣2)7. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )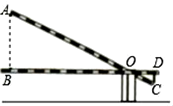 A、0.2m B、0.3m C、0.4m D、0.5m8. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A、0.2m B、0.3m C、0.4m D、0.5m8. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )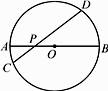 A、 B、2 C、2 D、89. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )
A、 B、2 C、2 D、89. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是直线x=1,下列结论正确的是( )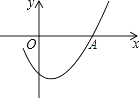 A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=010. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
A、b2<4ac B、ac>0 C、2a﹣b=0 D、a﹣b+c=010. 利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 .如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 11. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
11. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )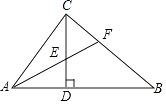 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 因式分解: .13. 我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为尺,竿子长为尺.
14. 如图,在正方形ABCD中,AD= ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为.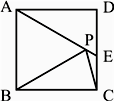 15. 已知点A为双曲线y= 图象上的点,点O为坐标原点,过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为5,则k的值为 .
15. 已知点A为双曲线y= 图象上的点,点O为坐标原点,过点A作AB⊥x轴于点B,连接OA.若△AOB的面积为5,则k的值为 .三、解答题
-
16. 计算:| ﹣2|+sin60°﹣ ﹣(﹣1 )2+2﹣217. 解方程: .18. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数
频数
频率

请根据以上信息,解答下列问题:
(1)、写出 的值并补全频数分布直方图;(2)、本市约有 名教师,用调查的样本数据估计日行走步数超过 步(包含 步)的教师有多少名?
(3)、若在 名被调查的教师中,选取日行走步数超过 步(包含 步的两名教师与大家分享心得,求被选取的两名教师恰好都在 步(包含 步)以上的概率.19. 一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量 (升)关于加满油后已行驶的路程 (千米)的函数图象.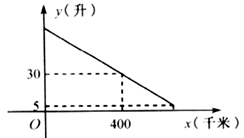 (1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.20. 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数 (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)、根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;(2)、求 关于 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.20. 已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数 (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6. (1)、求一次函数与反比例函数的解析式;(2)、求两函数图象的另一个交点坐标;
(1)、求一次函数与反比例函数的解析式;(2)、求两函数图象的另一个交点坐标;
(3)、直接写出不等式;kx+b≤ 的解集.21. 如图,在Rt△ACB中,∠C=90°,AC=3 cm,BC=4 cm,以BC为直径作⊙O交AB于点D.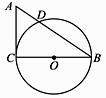 (1)、求线段AD的长度;(2)、点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.22. 如图,已知二次函数y=ax2+ x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)、求线段AD的长度;(2)、点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.22. 如图,已知二次函数y=ax2+ x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.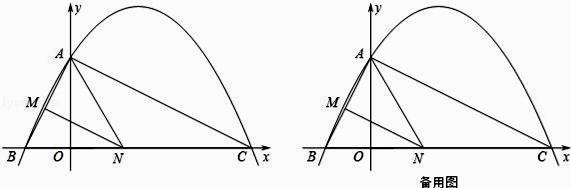 (1)、请直接写出二次函数y=ax2+ x+c的表达式;
(1)、请直接写出二次函数y=ax2+ x+c的表达式;
(2)、判断△ABC的形状,并说明理由;
(3)、若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;(4)、若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.