备考2019年高考数学一轮专题:第19讲 函数y=Asin(ωx+φ)的图象及三角函数模型的简单应用
试卷更新日期:2018-11-01 类型:一轮复习
一、单选题
-
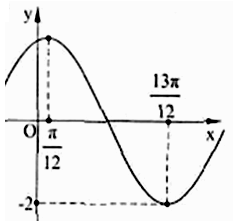
1. 将函数 的图象向右平移 个单位长度,所得图象对应的函数( )A、在区间 上单调递增 B、在区间 上单调递减 C、在区间 上单调递增 D、在区间 上单调递减2. 要想得到函数 的图象,只需将 的图像( )A、向左平移 个单位 B、向左平移 个单位 C、向右平移 个单位 D、向右平移 个单位3. 要得到函数 的图象,只需要将函数 的图象( )A、向上平移 个单位 B、向下平移 个单位 C、向左平移 个单位 D、向右平移 个单位4. 若将函数 的图象向左平移 个单位长度,则平移后图象的一条对称轴为( )A、 B、 C、 D、5. 将函数 的图像向左平移 个周期(即最小正周期)后,所得图像对应的函数为( )A、 B、 C、 D、6. 如图是函数 的图象,那么( )
 A、 B、 C、 D、7. 将函数y=sin(x+ )的图象上各点的纵坐标不变,横坐标缩短到原来的 倍,再向右平移 个单位,所得到的图象解析式是( )A、 B、 C、 D、8. 将函数f(x)=2sin 的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的 倍,所得图象关于直线x= 对称,则φ的最小正值为( )A、 B、 C、 D、9. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位10. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度
A、 B、 C、 D、7. 将函数y=sin(x+ )的图象上各点的纵坐标不变,横坐标缩短到原来的 倍,再向右平移 个单位,所得到的图象解析式是( )A、 B、 C、 D、8. 将函数f(x)=2sin 的图象向右平移φ(φ>0)个单位,再将图象上每一点横坐标缩短到原来的 倍,所得图象关于直线x= 对称,则φ的最小正值为( )A、 B、 C、 D、9. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位10. 要得到函数 的图象,只需将函数 的图象( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度二、填空题
-
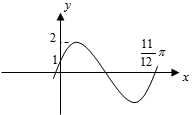
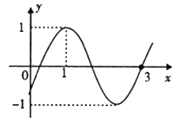
11. 已知函数f(x)=sin(ωx+φ)(ω>0)的图象如图所示,则f(4)= .
 12. 函数 的图像可由函数 的图像至少向右平移个单位长度得到.13. 已知函数y=sin(ωx+φ)(ω>0,|φ|< )的部分图象如图所示,则ω= , φ= .
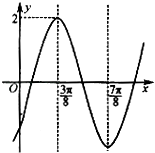
12. 函数 的图像可由函数 的图像至少向右平移个单位长度得到.13. 已知函数y=sin(ωx+φ)(ω>0,|φ|< )的部分图象如图所示,则ω= , φ= .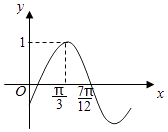 14. 函数 ( 是常数, , )的部分如右图,则 .
14. 函数 ( 是常数, , )的部分如右图,则 .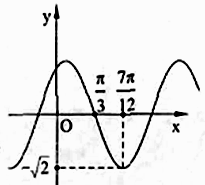 15. 用“五点法”作函数y=2sin(2x﹣ )的简图时,五个关键点的坐标分别是 .16. 已知函数 ,将其图像向右平移 个单位长度后得到函数 的图像,若函数 为奇函数,则 的最小值为 .
15. 用“五点法”作函数y=2sin(2x﹣ )的简图时,五个关键点的坐标分别是 .16. 已知函数 ,将其图像向右平移 个单位长度后得到函数 的图像,若函数 为奇函数,则 的最小值为 .三、解答题
-
17. 在[0,2π]内用五点法作出y=﹣sinx﹣1的简图.18. 已知函数(1)、求函数 的单调递减区间;(2)、将函数 的图像向左平移 个单位,再将所得图像上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数 的图像,求 在 上的值域.