2017年安徽省淮南市高考数学一模试卷(理科)
试卷更新日期:2017-03-15 类型:高考模拟
一、选择题
-
1. 已知集合A={x|x2≤1},B={x|x<a},若A∪B=B,则实数a的取值范围是( )A、(﹣∞,1) B、(﹣∞,﹣1] C、(1,+∞) D、[1,+∞)2. 若复数z满足i•z= (1+i),则z的虚部是( )A、﹣ i B、 i C、﹣ D、3. 《九章算术》是我国古代数学名著,也是古代东方数学的代表作.书中有如下问题:“今有勾八步,股一十五步,问勾中容圆,径几何?”其意思为:“已知直角三角形两直角边长分别为8步和15步,问其内切圆的直径为多少步?”现若向此三角形内投豆子,则落在其内切圆内的概率是( )A、 B、 C、 D、4. 阅读如图所示的程序框图,则该算法的功能是( )
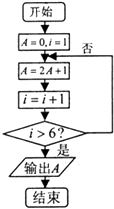 A、计算数列{2n﹣1}前5项的和 B、计算数列{2n﹣1}前5项的和 C、计算数列{2n﹣1}前6项的和 D、计算数列{2n﹣1}前6项的和5. 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),直线x= 是它的一条对称轴,且( ,0)是离该轴最近的一个对称中心,则φ=( )A、 B、 C、 D、6. 函数y= 的图象大致是( )A、
A、计算数列{2n﹣1}前5项的和 B、计算数列{2n﹣1}前5项的和 C、计算数列{2n﹣1}前6项的和 D、计算数列{2n﹣1}前6项的和5. 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),直线x= 是它的一条对称轴,且( ,0)是离该轴最近的一个对称中心,则φ=( )A、 B、 C、 D、6. 函数y= 的图象大致是( )A、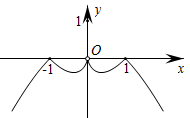
B、
B、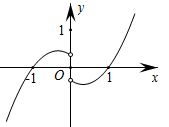
C、
C、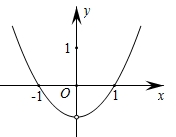
D、
D、
7. 函数y=f(x)在[0,2]上单调递增,且函数f(x+2)是偶函数,则下列结论成立的是( )A、f(1)<f( )<f( ) B、f( )<f(1)<f( ) C、f( )<f( )<f(1) D、f( )<f(1)<f( )8. 已知等差数列{an},{bn}的前n项和分别为Sn , Tn , 若对于任意的自然数n,都有 = ,则 + =( )A、 B、 C、 D、9. 设e是自然对数的底,a>0且a≠1,b>0且b≠1,则“loga2>logbe”是“0<a<b<1”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件10. 已知点F1、F2是双曲线C: =1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )A、(1,+∞) B、[ ,+∞) C、(1, ] D、(1, ]11. 设函数f(x)= ,则满足f(f(a))=2f(a)的a取值范围是( )A、[ ,+∞) B、[ ,1] C、[1,+∞) D、[0,1]12. 如果定义在R上的函数f(x)满足:对于任意x1≠x2 , 都有xlf(xl)+x2f(x2)≥xlf(x2)+x2f(xl),则称f(x)为“H函数”,给出下列函数:
7. 函数y=f(x)在[0,2]上单调递增,且函数f(x+2)是偶函数,则下列结论成立的是( )A、f(1)<f( )<f( ) B、f( )<f(1)<f( ) C、f( )<f( )<f(1) D、f( )<f(1)<f( )8. 已知等差数列{an},{bn}的前n项和分别为Sn , Tn , 若对于任意的自然数n,都有 = ,则 + =( )A、 B、 C、 D、9. 设e是自然对数的底,a>0且a≠1,b>0且b≠1,则“loga2>logbe”是“0<a<b<1”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件10. 已知点F1、F2是双曲线C: =1(a>0,b>0)的左、右焦点,O为坐标原点,点P在双曲线C的右支上,且满足|F1F2|=2|OP|,|PF1|≥3|PF2|,则双曲线C的离心率的取值范围为( )A、(1,+∞) B、[ ,+∞) C、(1, ] D、(1, ]11. 设函数f(x)= ,则满足f(f(a))=2f(a)的a取值范围是( )A、[ ,+∞) B、[ ,1] C、[1,+∞) D、[0,1]12. 如果定义在R上的函数f(x)满足:对于任意x1≠x2 , 都有xlf(xl)+x2f(x2)≥xlf(x2)+x2f(xl),则称f(x)为“H函数”,给出下列函数:①y=﹣x3+x+l;
②y=3x﹣2(sinx﹣cosx);
③y=l﹣ex;
④f(x)= ;
⑤y=
其中“H函数”的个数有( )
A、3个 B、2个 C、l个 D、0个二、填空题
-
13. 已知两个单位向量 , 的夹角为60°,则| +2 |= .14. 实数x,y满足 ,则 的取值范围是 .15. 若(x2﹣a)(x+ )10的展开式中x6的系数为30,则 (3x2+1)dx= .16. 已知函数f(x)= ,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 .
三、解答题
-
17. 在△ABC中,角A,B,C的对边分别是a,b,c,且 acosC=(2b﹣ c)cosA.(1)、求角A的大小;(2)、求cos( ﹣B)﹣2sin2 的取值范围.18. 数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* .
(Ⅰ)证明:数列{ }是等差数列;
(Ⅱ)设bn=3n• ,求数列{bn}的前n项和Sn .
19. 某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在[50,60),[90,100]的数据).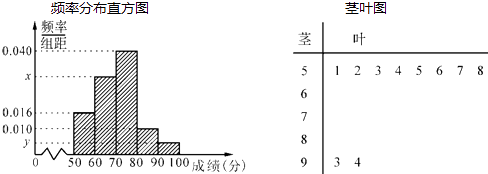
(Ⅰ)求样本容量n和频率分布直方图中x、y的值;
(Ⅱ)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动,设ξ表示所抽取的3名同学中得分在[80,90)的学生个数,求ξ的分布列及其数学期望.
20. 设椭圆E的方程为 +y2=1(a>1),O为坐标原点,直线l与椭圆E交于点A,B,M为线段AB的中点.(1)、若A,B分别为E的左顶点和上顶点,且OM的斜率为﹣ ,求E的标准方程;(2)、若a=2,且|OM|=1,求△AOB面积的最大值.21. 已知函数f(x)=xe2x﹣lnx﹣ax.(1)、当a=0时,求函数f(x)在[ ,1]上的最小值;(2)、若∀x>0,不等式f(x)≥1恒成立,求a的取值范围;(3)、若∀x>0,不等式f( )﹣1≥ e + 恒成立,求a的取值范围.