2015-2016学年河南省周口市周口港区八年级下学期期中数学试卷

试卷更新日期：2017-03-15 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各式与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{8}$ C、 $\sqrt{2}$ D、 $\sqrt{12}$

查看试题解析
2. 要使二次根式 $\sqrt{x - 2}$ 有意义，x必须满足（）

A、x≤2 B、x≥2 C、x＞2 D、x＜2

查看试题解析
3. 实数a在数轴上的位置如图所示，则化简|1﹣a|+ $\sqrt{{(a - 2)}^{2}}$ 的结果是（）

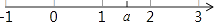A、﹣1 B、1 C、2a﹣3 D、3﹣2a

查看试题解析
4. 在平面直角坐标系中，点P（﹣x，2x）到原点O的距离等于5，则x的值是（）

A、±1 B、1 C、 $\sqrt{5}$ D、± $\sqrt{5}$

查看试题解析
5. 等腰三角形的腰长为5，底边长为8，则该三角形的面积等于（）

A、6 B、12 C、24 D、40

查看试题解析
6. 如图，四边形ABCD的对角线AC和BD交于点O，则下列不能判断四边形ABCD是平行四边形的条件是（）

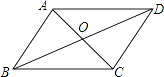A、OA=OC，AD∥BC B、∠ABC=∠ADC，AD∥BC C、AB=DC，AD=BC D、∠ABD=∠ADB，∠BAO=∠DCO

查看试题解析
7. 如图，在四边形ABCD的外侧，以四边形的边为边分别作四个小正方形，连接相邻的两个顶点，得到四个阴影三角形，则这四个阴影三角形的面积a、b、c、d满足（）

A、a+b=c+d B、a²+b²=c²+d² C、a+c=b+d D、a²+c²=b²+d²

查看试题解析

二、填空题：

8. 计算： $\sqrt{3 \times 6}$ = ．

查看试题解析
9. 当m= $\sqrt{3} - 1$ 时，代数式m²+2m﹣2的值是．

查看试题解析
10. 命题“在同一个三角形中，等边对等角”的逆命题是，是（填“真命题”或“假命题”）

查看试题解析
11. 在Rt△ABC中，∠C=90°，∠B=60°，AC=2，则斜边AB的长为．

查看试题解析
12. 若▱ABCD的三条边分别为8cm，（x﹣2）cm，（x+3）cm，则该▱ABCD的周长是 cm．

查看试题解析
13. 在▱ABCD中，边AB=3，对角线AC=2 $\sqrt{5}$ ，BD=4，则▱ABCD的面积等于．

查看试题解析
14. 如图，在△ABC中，AB=AC=4，BD是△ABC的中线，∠ADB=120°，点E在中线BD的延长线上，则△ACE是直角三角形时，DE的长为．

查看试题解析

三、解答题：

15. 计算题：

(1)、（ $\sqrt{50} - \sqrt{18}$ ） $\div \sqrt{2} \times \frac{1}{\sqrt{2}}$ ；

(2)、4a² $\sqrt{\frac{1}{8 a}} - 7 \sqrt{2 a^{3}}$ ．

查看试题解析
16. 计算：

(1)、已知m=1+ $\sqrt{3}$ ，n=1﹣ $\sqrt{3}$ ，求代数式m²+2mn﹣n²的值；

(2)、已知x+ $\frac{1}{x}$ = $\sqrt{10}$ ，求代数式x﹣ $\frac{1}{x}$ 的值．

查看试题解析
17. 如图，在四边形ABCD中，∠D=90°，AB=2，BC=4，CD=AD= $\sqrt{6}$ ．

(1)、求∠BAD、∠BCD的度数．

(2)、求四边形ABCD的面积．

查看试题解析
18. 完成下列证明过程，求证：三角形的中位线平行于三角形的第三边，并且等于第三边的一半．
已知：
求证：

查看试题解析
19. 如图，在▱ABCD中，∠ADC的平分线交AB于点E，∠ABC的平分线交CD于点F，求证：四边形EBFD是平行四边形．

查看试题解析
20. 如图，△ACB与△ECD都是等腰直角三角形，△ACB的顶点A在△ECD的斜边DE上，求证：AE²+AD²=2AC² ．（提示：连接BD）

查看试题解析
21. 解答题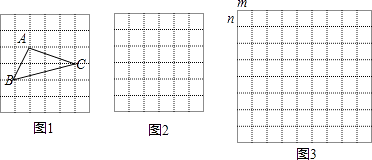

(1)、在△ABC中，AB、BC、AC三边的长分别为 $\sqrt{5}$ 、 $\sqrt{17}$ 、 $\sqrt{10}$ ，求这个三角形的面积．
如图1，某同学在解答这道题时，先建立一个每个小正方形的边长都是1的网格，再在网格中画出边长符合要求的格点三角形ABC（即△ABC三个顶点都在小正方形的顶点处），这样不需要求△ABC的高，而借用网格就能就算出它的面积．
请你将△ABC的面积直接填写在横线上．

(2)、思维拓展：
已知△ABC三边的长分别为 $\sqrt{13} a 、 2 \sqrt{2} a 、 \sqrt{17}$ a（a＞0），求这个三角形的面积．
我们把上述求△ABC面积的方法叫做构图法．如图2，网格中每个小正方形的边长都是a，请在网格中画出相应的△ABC，并求出它的面积．

(3)、类比创新：
若△ABC三边的长分别为 $\sqrt{m^{2} + 16 n^{2}} ， \sqrt{16 m^{2} + 9 n^{2}} ， \sqrt{9 m^{2} + n^{2}}$ （m＞0，n＞0，且m≠n），求出这个三角形的面积．
如图3，网格中每个小长方形长、宽都是m，n，请在网格中画出相应的△ABC，用网格计算这个三角形的面积．

查看试题解析
22.
如图，在△ABC中，AC的中点为D，BC的中点为E，F是DE的中点，动点G在边AB上，连接GF，延长GF到点H，使HF=GF，连接HD，HE．

(1)、求证：四边形HDGE是平行四边形．

(2)、已知∠C=90°，∠A=30°，AB=4．
①当AG为何值时，四边形HDGE是矩形；
②当AG为何值时，四边形HDGE是菱形．

查看试题解析