人教版九年级数学上册第二十三章旋转单元检测b卷

试卷更新日期：2018-10-30 类型：单元试卷

进入出卷网下载

一、选择题

1. 如果4张扑克按图1的形式摆放在桌面上，将其中一张旋转180°后，扑克的放置情况如图2所示，那么旋转的扑克从左起是（）

A、第一张 B、第二张 C、第三张 D、第四张

查看试题解析
2. 下列现象属于旋转的是（）

A、摩托车在急刹车时向前滑动 B、幸运大转盘转运的过程 C、飞机起飞后冲向空中的过程 D、笔直的铁轨上飞驰而过的火车

查看试题解析
3. 如图，按a，b，c的排列规律，在空格d上的图形应该是（）

A、 B、 C、 D、

查看试题解析
4. 在平面直角坐标系中，若点P（x，y）在第二象限，且|x|﹣1=0，y²﹣4=0，则点P关于坐标原点对称的点P′的坐标是（）

A、P′（﹣1，﹣2） B、P′（1，﹣2） C、P′（﹣1，2） D、P′（1，2）

查看试题解析
5. 若点P（m，2）与点Q（3，n）关于原点对称，则m，n的值分别为（）

A、﹣3，2 B、3，﹣2 C、﹣3，﹣2 D、3，2

查看试题解析
6. 如图，若正六边形ABCDEF绕着中心点O旋转α度后得到的图形与原来图形重合，则α的最小值为（）

A、120° B、90° C、45° D、60°

查看试题解析
7. 如图，网格纸上正方形小格的边长为1．图中线段AB和点P绕着同一个点做相同的旋转，分别得到线段A′B′和点P′，则点P′所在的单位正方形区域是（）

A、1 区 B、2 区 C、3 区 D、4 区

查看试题解析
8. 如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么点A（﹣1，3）的对应点A′的坐标是（）

A、（3，1） B、（1，3） C、（﹣3，1） D、（﹣1，﹣3）

查看试题解析
9. 将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，如图，则∠EDP的大小为（）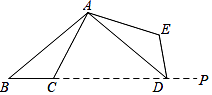

A、80° B、100° C、120° D、不能确定

查看试题解析
10. 如图，在Rt△ABC中，∠C=90°，M为AB边的中点，将Rt△ABC绕点M旋转，使点C与点A重合得△DEA，AE交CB于点N．若AB=2 $\sqrt{13}$ ，AC=4，则CN的长为（）

A、 $\frac{10}{3}$ B、 $\frac{2}{3}$ C、 $\frac{4}{3}$ D、 $\frac{5}{3}$

查看试题解析

二、填空题

11. 时钟的时针在不停地旋转，从下午3时到下午6时（同一天），时针旋转的角度是．

查看试题解析
12. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C'，连接AA′，若∠1=25°，则∠BAA'的度数是．

查看试题解析
13. 已知：如图，在平面直角坐标系xOy中，点B₁、点C₁的坐标分别为（1，0），（1， $\sqrt{3}$ ），将△OB₁C₁绕原点O逆时针旋转60°，再将其各边都扩大为原来的m倍，使OB₂=OC₁ ，得到△OB₂C₂ ．将△OB₂C₂绕原点O逆时针旋转60°，再将其各边都扩大为原来的m倍，使OB₃=OC₂ ，得到△OB₃C₃ ，如此下去，得到△OB₂₀₁₁C₂₀₁₁ ，则点C₂₀₁₁的坐标：．

查看试题解析
14. 将线段OB绕点O逆时针旋转60°得到线段OC，继续旋转α（0°＜α＜120°）得到线段OD，连接CD．

(1)、如图，连接BD，则∠BDC=（度）；

(2)、将线段OB放在平面直角坐标系中，O是坐标原点，点B的坐标为（﹣6，0），以OB为斜边作Rt△OBE，使∠OBE=∠OCD，且点E在第三象限，若∠CED=90°，则α的大小=（度），点D的坐标为．

查看试题解析
15. 图中，甲图怎样变成乙图：．

查看试题解析
16. △ABC中，∠ACB=120°，将它绕着点C逆时针旋转30°后得到△DCE，则∠ACE的度数为．

查看试题解析

三、解答题

17. 如图，已知△ABC和△AEF中，∠B=∠E，AB=AE，BC=EF，∠EAB=25°，∠F=57°；

(1)、请说明∠EAB=∠FAC的理由；

(2)、△ABC可以经过图形的变换得到△AEF，请你描述这个变换；

(3)、求∠AMB的度数．

查看试题解析
18. 如图

(1)、如图，已知△ABC，请你作出AB边上的高CD，AC边上的中线BE，角平分线AF（不写作法，保留痕迹）

(2)、如图，直线l表示一条公路，点A，点B表示两个村庄．现要在公路上造一个车站，并使车站到两个村庄A，B的距离之和最短，问车站建在何处？请在图上标明地点，并说明理由．（要求尺规作图，不写作法）

查看试题解析
19. 下列图形是中心对称图形吗？如果是中心对称图形，在图中用点O标出对称中心．

查看试题解析
20. 在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90度．

(1)、判断下列命题的真假（在相应的括号内填上“真”或“假”）．
①等腰梯形是旋转对称图形，它有一个旋转角为180度．（）
②矩形是旋转对称图形，它有一个旋转角为180°．（）

(2)、填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是（写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形．

(3)、写出两个多边形，它们都是旋转对图形，都有一个旋转角为72°，并且分别满足下列条件：
①是轴对称图形，但不是中心对称图形：；
②既是轴对称图形，又是中心对称图形：．

查看试题解析
21. 如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴，垂足为A．

(1)、将点B绕原点逆时针方向旋转90°后记作点C，求点C的坐标；

(2)、△O′A′B′与△OAB关于原点对称，写出点B′、A′的坐标．

查看试题解析
22. 当m为何值时

(1)、点A（2，3m）关于原点的对称点在第三象限；

(2)、点B（3m﹣1，0.5m+2）到x轴的距离等于它到y轴距离的一半？

查看试题解析
23. 在直角坐标平面内，已知点A（3，0）、B（2，3），点B关于原点对称点为C．

(1)、写出C点的坐标；

(2)、求△ABC的面积．

查看试题解析
24. 等边△OAB在平面直角坐标系中，已知点A（2，0），将△OAB绕点O顺时针方向旋转a°（0＜a＜360）得△OA₁B₁ ．

(1)、求出点B的坐标；

(2)、当A₁与B₁的纵坐标相同时，求出a的值；

(3)、在（2）的条件下直接写出点B₁的坐标．

查看试题解析

人教版九年级数学上册 第二十三章旋转 单元检测b卷

一、选择题

二、填空题

三、解答题

人教版九年级数学上册第二十三章旋转单元检测b卷