人教版九年级数学上册 第二十三章旋转 单元检测a卷
试卷更新日期:2018-10-30 类型:单元试卷
一、选择题
-
1. 下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面的图形中必须由“基本图形”既平移又旋转而形成的图形是( )A、
2. 下面的图形中必须由“基本图形”既平移又旋转而形成的图形是( )A、 B、
B、 C、
C、 D、
D、 3. 国旗上的四个小五角星,通过怎样的移动可以相互得到( )A、轴对称 B、平移 C、旋转 D、平移和旋转4. 在平面直角坐标系中,点P(﹣2,3)与点Q关于原点对称,则点Q的坐标为( )A、(﹣2,﹣3) B、(3,﹣2) C、(2,3) D、(2,﹣3)5. 点P(﹣2,1)关于原点对称的点的坐标是( )A、(2,1) B、(2,﹣1) C、(﹣1,2) D、(1,﹣2)6. 如果一个图形绕着一个点至少需要旋转72°才能与它本身重合,则下列说法正确的是( )A、这个图形一定是中心对称图形 B、这个图形可能是中心对称图形 C、这个图形旋转216°后能与它本身重合 D、以上都不对7. 如图,△ODC是由△OAB绕点O顺时针旋转50°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为130°,则∠C的度数是( )
3. 国旗上的四个小五角星,通过怎样的移动可以相互得到( )A、轴对称 B、平移 C、旋转 D、平移和旋转4. 在平面直角坐标系中,点P(﹣2,3)与点Q关于原点对称,则点Q的坐标为( )A、(﹣2,﹣3) B、(3,﹣2) C、(2,3) D、(2,﹣3)5. 点P(﹣2,1)关于原点对称的点的坐标是( )A、(2,1) B、(2,﹣1) C、(﹣1,2) D、(1,﹣2)6. 如果一个图形绕着一个点至少需要旋转72°才能与它本身重合,则下列说法正确的是( )A、这个图形一定是中心对称图形 B、这个图形可能是中心对称图形 C、这个图形旋转216°后能与它本身重合 D、以上都不对7. 如图,△ODC是由△OAB绕点O顺时针旋转50°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为130°,则∠C的度数是( ) A、25° B、30° C、35° D、40°8. 如图,把△ABC经过一定的变化得到△A′B′C′,如果△ABC上点P的坐标为(x,y),那么这个点在△A′B′C′中的对应点P′的坐标为( )
A、25° B、30° C、35° D、40°8. 如图,把△ABC经过一定的变化得到△A′B′C′,如果△ABC上点P的坐标为(x,y),那么这个点在△A′B′C′中的对应点P′的坐标为( ) A、(﹣x,y﹣2) B、(﹣x+2,y+2) C、(﹣x+2,﹣y) D、(﹣x,y+2)9. 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1 , 若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A、(﹣x,y﹣2) B、(﹣x+2,y+2) C、(﹣x+2,﹣y) D、(﹣x,y+2)9. 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1 , 若点B1在线段BC的延长线上,则∠BB1C1的大小为( )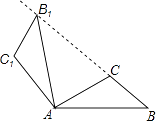 A、70° B、80° C、84° D、86°10. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E,若AD=BE,则△A′DE的面积是( )
A、70° B、80° C、84° D、86°10. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E,若AD=BE,则△A′DE的面积是( ) A、3 B、5 C、11 D、6
A、3 B、5 C、11 D、6二、填空题
-
11. 如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是米.
 12. 将一副三角板的两个直角顶点叠放在一起拼成如下的图形.若∠EAB=40°,则∠CAD=;将△ABC绕直角顶点A旋转时,保持AD在∠BAC的内部,设∠EAC=x°,∠BAD=y°,则x与y的关系是 .
12. 将一副三角板的两个直角顶点叠放在一起拼成如下的图形.若∠EAB=40°,则∠CAD=;将△ABC绕直角顶点A旋转时,保持AD在∠BAC的内部,设∠EAC=x°,∠BAD=y°,则x与y的关系是 . 13. 如图,在直角坐标系中,已知点P0的坐标为(1,0),以O旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3 , OP4 , OPn(n为正整数),则点P6的坐标是;△P5OP6的面积是 .
13. 如图,在直角坐标系中,已知点P0的坐标为(1,0),以O旋转中心,将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3 , OP4 , OPn(n为正整数),则点P6的坐标是;△P5OP6的面积是 .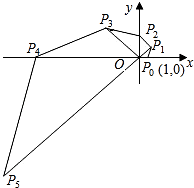 14. 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .
14. 如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 . 15. 如图,五角星也可以看作是一个三角形绕中心O旋转次得到的,每次旋转角度是 .
15. 如图,五角星也可以看作是一个三角形绕中心O旋转次得到的,每次旋转角度是 . 16. 如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC= .
16. 如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC= .
三、解答题
-
17. 如图,正方形ABCD边长为2cm,以各边中心为圆心,1cm为半径依次作 圆,将正方形分成四部分.
 (1)、这个图形旋转对称图形(填“是”或“不是”);若是,则旋转中心是点 , 最小旋转角是度.(2)、求图形OBC的周长和面积.18. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,2),B(3,4),请在所给网格上按要求画整点四边形.
(1)、这个图形旋转对称图形(填“是”或“不是”);若是,则旋转中心是点 , 最小旋转角是度.(2)、求图形OBC的周长和面积.18. 在直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形.如图,已知整点A(1,2),B(3,4),请在所给网格上按要求画整点四边形.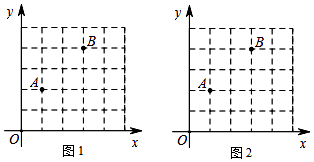 (1)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(2)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.19. 如图,已知△ABC与△A′B′C′成中心对称图形,求出它的对称中心O.
(1)、在图1中画一个四边形OABP,使得点P的横、纵坐标之和等于5.(2)、在图2中画一个四边形OABQ,使得点Q的横、纵坐标的平方和等于20.19. 如图,已知△ABC与△A′B′C′成中心对称图形,求出它的对称中心O.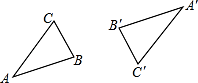 20. 图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,面积为74的正方形.在Rt△ABC中,若直角边BC=5,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到图乙所示的“数学风车”.
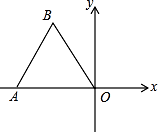
20. 图甲是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成,面积为74的正方形.在Rt△ABC中,若直角边BC=5,将四个直角三角形中边长为5的直角边分别向外延长一倍,得到图乙所示的“数学风车”. (1)、这个风车至少需要绕着中心旋转才能和本身重合;(2)、求这个风车的外围周长(图乙中的实线).21. 如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1 , 求点B1的坐标.
(1)、这个风车至少需要绕着中心旋转才能和本身重合;(2)、求这个风车的外围周长(图乙中的实线).21. 如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1 , 求点B1的坐标.