浙江省金华十五中2019届九年级上学期数学第一次月考试卷(浙教一、二章)
试卷更新日期:2018-10-30 类型:月考试卷
一、单选题
-
1. 下列函数关系中,不属于二次函数的是( )
A、 B、 C、 D、2. 小亮和小刚按如下规则做游戏:每人从1,2,…,12中任意选择一个数,然后两人各掷一次均匀的骰子,谁事先选择的数等于两人掷得的点数之和谁就获胜;如果两人选择的数都不等于掷得的点数之和,就再做一次上述游戏,直至决出胜负.从概率的角度分析,游戏者事先选择( )获胜的可能性较大.
A、5 B、6 C、7 D、83. 对于二次函数 的图象,下列说法正确的是( )
A、开口向下 B、当 时, 有最大值是 C、对称轴是 D、顶点坐标是4. 在不透明的盒子中装有3个红球,2个白球,它们除颜色外均相同,则从盒中子任意摸出一个球是白球的概率是( )
A、 B、 C、 D、5. 二次函数 (a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b> ;④a-b+c>0;⑤若 , 且 , 则 .其中正确的有( ). A、①②③ B、②④ C、②⑤ D、②③⑤6. 已知抛物线 过 、 、 、 四点,则 与 的大小关系是( )
A、①②③ B、②④ C、②⑤ D、②③⑤6. 已知抛物线 过 、 、 、 四点,则 与 的大小关系是( )
A、 > B、 = C、 < D、不能确定7. 在一个不透明的口袋中装有12个白球、16个黄球、24个红球、28个绿球,除颜色其余都相同,小明通过多次摸球实验后发现,摸到某种颜色的球的频率稳定在0.3左右,则小明做实验时所摸到的球的颜色是( )A、白色 B、黄色 C、红色 D、绿色8. 把抛物线 向下平移 个单位长度,再向右平移 个单位长度,所得抛物线是( )
A、 B、 C、 D、9. 甲乙两人做游戏,同时掷两枚相同的硬币,双方约定:同面朝上甲胜,异面朝上则乙胜,则这个游戏对双方( )A、公平 B、对甲有利 C、对乙有利 D、无法确定公平性二、填空题
-
10. 二次函数 的顶点坐标是 .
11. 若二次函数 的图象经过原点,则 的值为 .12. 已知二次函数 有最大值 ,则 , 的大小关系为 .
13. 将函数 所在的坐标系先向左平移 个单位再向下平移 个单位,则函数在新坐标系中的函数关系式是 .
14. 经过 , , 点的抛物线解析式是 .
15. 如图,抛物线y=x2+bx+ 与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第一象限).抛物线的顶点C在直线OB上,对称轴与x轴相交于点D.平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为 .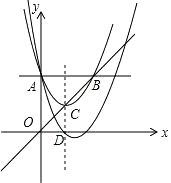 16. 将二次函数式 配方成顶点式后,结果是 .
16. 将二次函数式 配方成顶点式后,结果是 .
17. 矩形的周长为 ,当矩形的长为 时,面积有最大值是 .
18. 如图,已知二次函数 的图象与 轴交于 , 两点,与 轴交于点 ,则二次函数的图象的顶点坐标是 .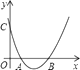 19. 广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度 (米)关于水珠与喷头的水平距离 (米)的函数解析式是 .水珠可以达到的最大高度是(米).
19. 广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度 (米)关于水珠与喷头的水平距离 (米)的函数解析式是 .水珠可以达到的最大高度是(米).
三、解答题
-
20. 在直角坐标平面内,点 为坐标原点,二次函数 的图象交 轴于点 、 ,且 .
(1)、求二次函数解析式;(2)、将上述二次函数图象沿 轴向右平移 个单位,设平移后的图象与 轴的交点为 ,顶点为 ,求 的面积.
21. 如图,在 中, ,点 在 上, ,交 与点 ,点 在 上, ,若 , , , ,求 与 的函数关系式,并写出自变量 的取值范围.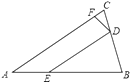 22. 如图,在平面直角坐标系 中,边长为 的正方形 的顶点 、 分别在 轴正半轴、 轴的负半轴上,二次函数 的图象经过 、 两点.
22. 如图,在平面直角坐标系 中,边长为 的正方形 的顶点 、 分别在 轴正半轴、 轴的负半轴上,二次函数 的图象经过 、 两点.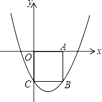 (1)、求该二次函数的顶点坐标;(2)、结合函数的图象探索:当 时 的取值范围;(3)、设 ,且 , 两点都在该函数图象上,试比较 、 的大小,并简要说明理由.23. 二次函数 的部分图象如图所示,其中图象与 轴交于点 ,与 轴交于点 ,且经过点 .
(1)、求该二次函数的顶点坐标;(2)、结合函数的图象探索:当 时 的取值范围;(3)、设 ,且 , 两点都在该函数图象上,试比较 、 的大小,并简要说明理由.23. 二次函数 的部分图象如图所示,其中图象与 轴交于点 ,与 轴交于点 ,且经过点 .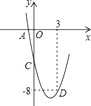 (1)、求此二次函数的解析式;
(1)、求此二次函数的解析式;
(2)、将此二次函数的解析式写成 的形式,并直接写出顶点坐标以及它与 轴的另一个交点 的坐标.(3)、利用以上信息解答下列问题:若关于 的一元二次方程 ( 为实数)在 的范围内有解,求 的取值范围
24. 有两个可以自由转动的均匀转盘,都被分成了 等份,并在每份内均标有数字,如图所示.规则如下:分别转动转盘,两个转盘停止后,将两个指针所指份内的数字相乘,(若指针停止在等分线上,那么重转一次,直到指针指向某份为止).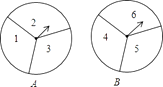 (1)、用列表或画树状图法分别求出数字之积为 的倍数和数字之积为 的倍数的概率;
(1)、用列表或画树状图法分别求出数字之积为 的倍数和数字之积为 的倍数的概率;
(2)、小明和小亮想用这两个转盘做游戏,他们规定:数字之积为 的倍数时,小明得 分;数字之积为 的倍数时,小亮得 分.这个游戏对双方公平吗?若认为公平请说明理由;若认为不公平,试修改得分规定,使游戏对双方公平.
25. 一家饰品店购进一种今年新上市的饰品进行销售,每件进价为 元,出于营销考虑,要求每件饰品的售价不低于 元且不高于 元,在销售过程中发现该饰品每周的销售量 (件)与每件饰品的售价 (元)之间满足一次函数关系:当销售单价为 元时,销售量为 件;当销售单价为 元时,销售量为 件.
(1)、请写出 与 的函数关系式;(2)、当饰品店每周销售这种饰品获得 元的利润时,每件饰品的销售单价是多少元?(3)、设该饰品店每周销售这种饰品所获得的利润为 元,将该饰品销售单价定为多少元时,才能使饰品店销售这种饰品所获利润最大?最大利润是多少?