人教版八年级数学上册 第十四章整式的乘法与因式分解 单元检测b卷
试卷更新日期：2018-10-29 类型：单元试卷
一、选择题
-
1. 下列各式，计算结果为3﹣2的是（ ）A、34÷36 B、36÷34 C、33÷36 D、（﹣3）×（﹣3）2. 下列运算结果正确的是（ ）A、a3+a4=a7 B、a4÷a3=a C、a3•a2=2a3 D、（a3）3=a63. 已知a2+b2=6ab且a＞b＞0，则 的值为（ ）A、 B、± C、2 D、±24. 若关于x的多项式x2﹣px﹣6含有因式x﹣2，则实数p的值为（ ）A、﹣5 B、5 C、﹣1 D、15. 若（ambn）3=a9b15 ， 则m、n的值分别为（ ）A、9；5 B、3；5 C、5；3 D、6；126. 分解因式b2（x﹣3）+b（x﹣3）的正确结果是（ ）A、（x﹣3）（b2+b） B、b（x﹣3）（b+1） C、（x﹣3）（b2﹣b） D、b（x﹣3）（b﹣1）7. 如果自然数a是一个完全平方数，那么与a之差最小且比a大的一个完全平方数是（ ）A、a+1 B、a2+1 C、a2+2a+1 D、a+2 +18. 在边长为a的正方形中挖掉一个边长为b的小正方形（a＞b）．把余下的部分剪拼成一个矩形（如图）．通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（ ）
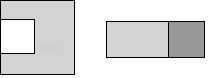A、a2﹣b2=（a+b）（a﹣b） B、（a+b）2=a2+2ab+b2 C、（a﹣b）2=a2﹣2ab+b2 D、a2﹣ab=a（a﹣b）9. 若a2﹣b2= ，a+b= ，则a﹣b的值为（ ）A、﹣ B、 C、1 D、210. 不论x取何值，x﹣x2﹣1的值都（ ）A、大于等于﹣ B、小于等于﹣ C、有最小值﹣ D、恒大于零二、填空题
-
11. 分解因式：3x2﹣6x2y+3xy2= ．12. 计算2x4•x3的结果等于 ．13. 已知am=3，an=2，则a2m﹣n的值为 ．
14. 如果代数﹣2y2+y﹣1的值为7，那么代数式4y2﹣2y+5的值为 ．15. 化简：a+1+a（a+1）+a（a+1）2+…+a（a+1）99= ．16. 若m=4n+3，则m2﹣8mn+16n2的值是 ．三、解答题
-
17. 计算：（a+b）2﹣a（a+2b+1）18. 已知：多项式A=b3﹣2ab(1)、请将A进行因式分解：(2)、若A=0且a≠0，b≠0，求 的值．19. 已知am=3，an=6，ak=4，求am+n+k的值．20. 计算0.1259×（﹣8）10+（ ）11×（2 ）12 ．21. 因式分解
(1)、10a（x﹣y）2+5ax（y﹣x）(2)、（x+y）2﹣10（x+y）+25．22. 阅读并完成下列各题：通过学习，同学们已经体会到灵活运用整式乘法公式给计算和化简带来的方便、快捷．相信通过下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．
【例】用简便方法计算995×1005．
解：995×1005
=（1000﹣5）（1000+5）①
=10002﹣52②
=999975．
(1)、例题求解过程中，第②步变形是利用（填乘法公式的名称）；(2)、用简便方法计算：①9×11×101×10 001；
②（2+1）（22+1）（24+1）…（232+1）+1．
23. 先化简，再求值：（3a﹣2）2﹣9a（a﹣5b）+12a5b2÷（﹣a2b）2 ， 其中ab=﹣ ．24. 问题再现：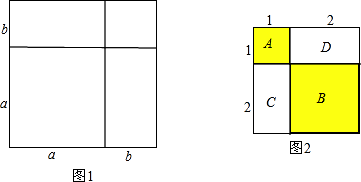
数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
例如：利用图形的几何意义证明完全平方公式．
证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：
这个图形的面积可以表示成：
（a+b）2或 a2+2ab+b2
∴（a+b）2 =a2+2ab+b2
这就验证了两数和的完全平方公式．
类比解决：
①请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）
问题提出：如何利用图形几何意义的方法证明：13+23=32？
如图2，A表示1个1×1的正方形，即：1×1×1=13
B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=23
而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
由此可得：13+23=（1+2）2=32
尝试解决：
②请你类比上述推导过程，利用图形的几何意义确定：13+23+33= ▲ ． （要求写出结论并构造图形写出推证过程）．
问题拓广：
③请用上面的表示几何图形面积的方法探究：13+23+33+…+n3= ▲ ． （直接写出结论即可，不必写出解题过程）