2016年四川省绵阳市中考数学试卷

试卷更新日期：2017-03-14 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣4的绝对值是（）

A、4 B、﹣4 C、 $\frac{1}{4}$ D、﹣ $\frac{1}{4}$

查看试题解析
2. 下列计算正确的是（）

A、x²+x⁵=x⁷ B、x⁵﹣x²=3x C、x²•x⁵=x¹⁰ D、x⁵÷x²=x³

查看试题解析
3. 下列图案，既是轴对称又是中心对称的是（）

A、 B、 C、 D、

查看试题解析
4. 如图是一个由7个相同正方体组合而成的几何体，它的主视图为（）

A、 B、 C、 D、

查看试题解析
5. 若关于x的方程x²﹣2x+c=0有一根为﹣1，则方程的另一根为（）

A、﹣1 B、﹣3 C、1 D、3

查看试题解析
6. 如图，沿AC方向开山修建一条公路，为了加快施工进度，要在小山的另一边寻找点E同时施工，从AC上的一点B取∠ABD=150°，沿BD的方向前进，取∠BDE=60°，测得BD=520m，BC=80m，并且AC，BD和DE在同一平面内，那么公路CE段的长度为（）

A、180m B、260 $\sqrt{3}$ m C、（260 $\sqrt{3}$ ﹣80）m D、（260 $\sqrt{2}$ ﹣80）m

查看试题解析
7. 如图，平行四边形ABCD的周长是26cm，对角线AC与BD交于点O，AC⊥AB，E是BC中点，△AOD的周长比△AOB的周长多3cm，则AE的长度为（）

A、3cm B、4cm C、5cm D、8cm

查看试题解析
8. 在关于x，y的方程组 ${\begin{matrix} 2 x + y = m + 7 \\ x + 2 y = 8 - m \end{matrix}$ 中，未知数满足x≥0，y＞0，那么m的取值范围在数轴上应表示为（）

A、 B、 C、 D、

查看试题解析
9. 如图，△ABC中AB=AC=4，∠C=72°，D是AB中点，点E在AC上，DE⊥AB，则cosA的值为（）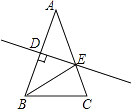

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} - 1}{4}$ C、 $\frac{\sqrt{5} + 1}{4}$ D、 $\frac{\sqrt{5} + 1}{2}$

查看试题解析
10. 有5张看上去无差别的卡片，上面分别写着1，2，3，4，5，随机抽取3张，用抽到的三个数字作为边长，恰能构成三角形的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{3}{20}$ C、 $\frac{7}{20}$ D、 $\frac{7}{10}$

查看试题解析
11. 如图，点E，点F分别在菱形ABCD的边AB，AD上，且AE=DF，BF交DE于点G，延长BF交CD的延长线于H，若 $\frac{A F}{D F}$ =2，则 $\frac{H F}{B G}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{7}{12}$ C、 $\frac{1}{2}$ D、 $\frac{5}{12}$

查看试题解析
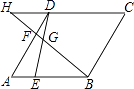12. 二次函数y=ax²+bx+c的图象如图所示，下列结论：①b＜2a；②a+2c﹣b＞0；③b＞a＞c；④b²+2ac＜3ab．其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 因式分解：2mx²﹣4mxy+2my²=

查看试题解析
14. 如图，AC∥BD，AB与CD相交于点O，若AO=AC，∠A=48°，∠D= ．

查看试题解析
15. 根据绵阳市统计年鉴，2014年末绵阳市户籍总人口数已超过548万人，548万人用科学记数法表示为人．

查看试题解析
16. △OAB三个顶点的坐标分别为O（0，0），A（4，6），B（3，0），以O为位似中心，将△OAB缩小为原来的 $\frac{1}{2}$ ，得到△OA′B′，则点A的对应点A′的坐标为．

查看试题解析
17. 如图，点O是边长为4 $\sqrt{3}$ 的等边△ABC的内心，将△OBC绕点O逆时针旋转30°得到△OB₁C₁ ， B₁C₁交BC于点D，B₁C₁交AC于点E，则DE= ．

查看试题解析
18.
如图所示的三角形数组是我国古代数学家杨辉发现的，称为杨辉三角形．现用A_i表示第三行开始，从左往右，从上往下，依次出现的第i个数，例如：A₁=1，A₂=2，A₃=1，A₄=1，A₅=3，A₆=3，A₇=1，则A₂₀₁₆= ．

查看试题解析

三、解答题

19. 计算：（π﹣3.14）⁰﹣| $\sqrt{12}$ sin60°﹣4|+（ $\frac{1}{2}$ ）^﹣¹ ．

查看试题解析
20. 先化简，再求值：（ $\frac{a + 1}{a^{2} - a}$ ﹣ $\frac{a - 1}{a^{2} - 2 a + 1}$ ）÷ $\frac{a - 1}{a}$ ，其中a= $\sqrt{3} + 1$ ．

查看试题解析
21. 绵阳七一中学开通了空中教育互联网在线学习平台，为了解学生使用情况，该校学生会把该平台使用情况分为A（经常使用）、B（偶尔使用）、C（不使用）三种类型，并设计了调查问卷、先后对该校初一（1）班和初一（2）班全体同学进行了问卷调查，并根据调查结果绘制成如下两幅不完整的统计图，请根据图中信息解答下列问题：

(1)、求此次被调查的学生总人数；

(2)、求扇形统计图中代表类型C的扇形的圆心角，并补全折线统计图；

(3)、若该校初一年级学生共有1000人，试根据此次调查结果估计该校初一年级中C类型学生约有多少人．

查看试题解析
22. 如图，直线y=k₁x+7（k₁＜0）与x轴交于点A，与y轴交于点B，与反比例函数y= $\frac{k^{2}}{x}$ （k₂＞0）的图象在第一象限交于C、D两点，点O为坐标原点，△AOB的面积为 $\frac{49}{2}$ ，点C横坐标为1．

(1)、求反比例函数的解析式；

(2)、如果一个点的横、纵坐标都是整数，那么我们就称这个点为“整点”，请求出图中阴影部分（不含边界）所包含的所有整点的坐标．

查看试题解析
23. 如图，AB为⊙O直径，C为⊙O上一点，点D是 $\hat{B C}$ 的中点，DE⊥AC于E，DF⊥AB于F．

(1)、判断DE与⊙O的位置关系，并证明你的结论；

(2)、若OF=4，求AC的长度．

查看试题解析
24. 绵阳人民商场准备购进甲、乙两种牛奶进行销售，若甲种牛奶的进价比乙种牛奶的进价每件少5元，其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同．

(1)、求甲种牛奶、乙种牛奶的进价分别是多少元？

(2)、若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件，两种牛奶的总数不超过95件，该商场甲种牛奶的销售价格为49元，乙种牛奶的销售价格为每件55元，则购进的甲、乙两种牛奶全部售出后，可使销售的总利润（利润=售价﹣进价）超过371元，请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案？

查看试题解析
25.
如图，抛物线y=ax²+bx+c（a≠0）与x轴交于A、B两点，与y轴交于点C（0，3），且此抛物线的顶点坐标为M（﹣1，4）．

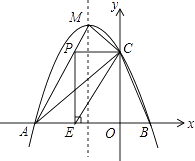(1)、求此抛物线的解析式；

(2)、设点D为已知抛物线对称轴上的任意一点，当△ACD与△ACB面积相等时，求点D的坐标；

(3)、点P在线段AM上，当PC与y轴垂直时，过点P作x轴的垂线，垂足为E，将△PCE沿直线CE翻折，使点P的对应点P′与P、E、C处在同一平面内，请求出点P′坐标，并判断点P′是否在该抛物线上．

查看试题解析
26.
如图，以菱形ABCD对角线交点为坐标原点，建立平面直角坐标系，A、B两点的坐标分别为（﹣2 $\sqrt{5}$ ，0）、（0，﹣ $\sqrt{5}$ ），直线DE⊥DC交AC于E，动点P从点A出发，以每秒2个单位的速度沿着A→D→C的路线向终点C匀速运动，设△PDE的面积为S（S≠0），点P的运动时间为t秒．

(1)、求直线DE的解析式；

(2)、求S与t之间的函数关系式，并写出自变量t的取值范围；

(3)、当t为何值时，∠EPD+∠DCB=90°？并求出此时直线BP与直线AC所夹锐角的正切值．

查看试题解析