2016年四川省广安市中考数学试卷
试卷更新日期:2017-03-14 类型:中考真卷
一、选择题
-
1. ﹣3的绝对值是( )A、 B、﹣3 C、3 D、±32. 下列运算正确的是( )A、(﹣2a3)2=﹣4a6 B、 =±3 C、m2•m3=m6 D、x3+2x3=3x33. 经统计我市去年共引进世界500强外资企业19家,累计引进外资410000000美元,数字410000000用科学记数法表示为( )A、41×107 B、4.1×108 C、4.1×109 D、0.41×1094. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 等边三角形
B、
等边三角形
B、 平行四边行
C、
平行四边行
C、 正五边形
D、
正五边形
D、 圆
5. 函数y= 中自变量x的取值范围在数轴上表示正确的是( )A、
圆
5. 函数y= 中自变量x的取值范围在数轴上表示正确的是( )A、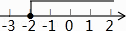 B、
B、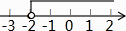 C、
C、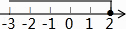 D、
D、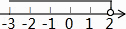 6. 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )A、7 B、10 C、35 D、707. 初三体育素质测试,某小组5名同学成绩如下所示,有两个数据被遮盖,如图:
6. 若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )A、7 B、10 C、35 D、707. 初三体育素质测试,某小组5名同学成绩如下所示,有两个数据被遮盖,如图:编号
1
2
3
4
5
方差
平均成绩
得分
38
34
■
37
40
■
37
那么被遮盖的两个数据依次是( )
A、35,2 B、36,4 C、35,3 D、36,38. 下列说法:①三角形的三条高一定都在三角形内
②有一个角是直角的四边形是矩形
③有一组邻边相等的平行四边形是菱形
④两边及一角对应相等的两个三角形全等
⑤一组对边平行,另一组对边相等的四边形是平行四边形
其中正确的个数有( )
A、1个 B、2个 C、3个 D、4个9. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ,则S阴影=( )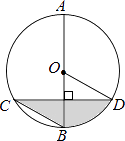 A、2π B、 π C、 π D、 π10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
A、2π B、 π C、 π D、 π10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
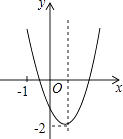 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 将点A(1,﹣3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到的点A′的坐标为 .12. 如图,直线l1∥l2 , 若∠1=130°,∠2=60°,则∠3= .
 13. 若反比例函数y= (k≠0)的图象经过点(1,﹣3),则一次函数y=kx﹣k(k≠0)的图象经过象限.14. 某市为治理污水,需要铺设一段全长600m的污水排放管道,铺设120m后,为加快施工进度,后来每天比原计划增加20m,结果共用11天完成这一任务,求原计划每天铺设管道的长度.如果设原计划每天铺设xm管道,那么根据题意,可列方程.15. 如图,三个正方形的边长分别为2,6,8;则图中阴影部分的面积为 .
13. 若反比例函数y= (k≠0)的图象经过点(1,﹣3),则一次函数y=kx﹣k(k≠0)的图象经过象限.14. 某市为治理污水,需要铺设一段全长600m的污水排放管道,铺设120m后,为加快施工进度,后来每天比原计划增加20m,结果共用11天完成这一任务,求原计划每天铺设管道的长度.如果设原计划每天铺设xm管道,那么根据题意,可列方程.15. 如图,三个正方形的边长分别为2,6,8;则图中阴影部分的面积为 . 16. 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):
16. 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):请依据上述规律,写出(x﹣ )2016展开式中含x2014项的系数是 .

三、解答题
-
17. 计算:( )﹣1﹣ +tan60°+|3﹣2 |.18. 先化简,再求值:( ﹣ )÷ ,其中x满足2x+4=0.19. 如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.
 20. 如图,一次函数y1=kx+b(k≠0)和反比例函数y2= (m≠0)的图象交于点A(﹣1,6),B(a,﹣2).
20. 如图,一次函数y1=kx+b(k≠0)和反比例函数y2= (m≠0)的图象交于点A(﹣1,6),B(a,﹣2). (1)、求一次函数与反比例函数的解析式;(2)、根据图象直接写出y1>y2时,x的取值范围.
(1)、求一次函数与反比例函数的解析式;(2)、根据图象直接写出y1>y2时,x的取值范围.四、实践应用
-
21. 某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
 (1)、初三(1)班接受调查的同学共有多少名;(2)、补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.22. 某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
(1)、初三(1)班接受调查的同学共有多少名;(2)、补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.22. 某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.甲
乙
丙
每辆汽车能装的数量(吨)
4
2
3
每吨水果可获利润(千元)
5
7
4
(1)、用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?(2)、水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)(3)、在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?23. 如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92) (1)、求点D与点C的高度差DH;(2)、求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米)24. 在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).
(1)、求点D与点C的高度差DH;(2)、求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米)24. 在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).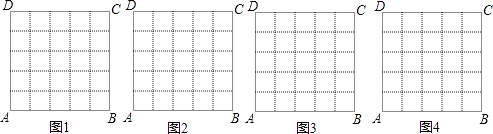
五、推理与论证
-
25. 如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
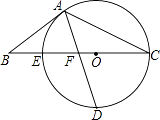 (1)、求证:AB是⊙O的切线;(2)、若CF=4,DF= ,求⊙O的半径r及sinB.
(1)、求证:AB是⊙O的切线;(2)、若CF=4,DF= ,求⊙O的半径r及sinB.六、拓展探究
-
26. 如图,抛物线y=x2+bx+c与直线y= x﹣3交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
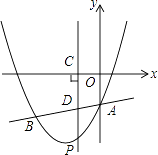 (1)、求抛物线的解析式;(2)、以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.(3)、当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.
(1)、求抛物线的解析式;(2)、以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.(3)、当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.
-