2017高考数学备考复习 易错题十五:几何证明选讲(选修4-1)
试卷更新日期:2017-03-14 类型:三轮冲刺
一、单选题
-
1.
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC=( )
 A、15° B、30° C、45° D、60°2. PT切⊙O于T,割线PAB经过O点交⊙O于A、B,若PT=4,PA=2,则cos∠BPT=( )
A、15° B、30° C、45° D、60°2. PT切⊙O于T,割线PAB经过O点交⊙O于A、B,若PT=4,PA=2,则cos∠BPT=( )
A、 B、 C、 D、3. 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2 . 则给出的下列结论中,错误的是( )
 A、AB=2 B、 C、∠E=30° D、△EBD∽△CDB4. 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
A、AB=2 B、 C、∠E=30° D、△EBD∽△CDB4. 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( ) A、70° B、64° C、62° D、51°5. 如图,△ABC内接于⊙O,∠A=40°,则∠OBC的度数为( )
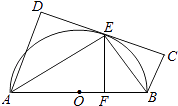
A、70° B、64° C、62° D、51°5. 如图,△ABC内接于⊙O,∠A=40°,则∠OBC的度数为( ) A、20° B、40° C、50° D、70°6. 如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:
A、20° B、40° C、50° D、70°6. 如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于E,过点B的圆的切线与AD的延长线交于点F,在上述条件下,给出下列四个结论:①BD平分∠CBF;
②FB2=FD•FA;
③AE•CE=BE•DE;
④AF•BD=AB•BF.

所有正确结论的序号是( )
A、①② B、③④ C、①②③ D、①②④7. 如图,已知圆的直径AB=13,C为圆上一点,过C作CD⊥AB于点D(AD>BD),若CD=6,则AD的长为( ) A、8 B、9 C、10 D、118. 如图,在圆的内接四边形ABCD中,AC平分∠BAD,EF切⊙O于C点,那么图中与∠DCF相等的角的个数是( )
A、8 B、9 C、10 D、118. 如图,在圆的内接四边形ABCD中,AC平分∠BAD,EF切⊙O于C点,那么图中与∠DCF相等的角的个数是( ) A、4 B、5 C、6 D、79. 直角梯形的一条对角线把梯形分成两个三角形,其中一个是边长为30的等边三角形,则这个梯形的中位线长是( )A、15 B、22.5 C、45 D、9010. 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,现有以下结论:①B,D两点间的距离为 ;②AD是该圆的一条直径;③CD= ;④四边形ABCD的面积S= .其中正确结论的个数为( )
A、4 B、5 C、6 D、79. 直角梯形的一条对角线把梯形分成两个三角形,其中一个是边长为30的等边三角形,则这个梯形的中位线长是( )A、15 B、22.5 C、45 D、9010. 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,现有以下结论:①B,D两点间的距离为 ;②AD是该圆的一条直径;③CD= ;④四边形ABCD的面积S= .其中正确结论的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. (几何证明选做题)
如图,弦AB与CD相交于⊙O内一点E,过E作BC的平行线与AD的延长线相交于点P.已知PD=2DA=2,则PE= .
 12. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:
12. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:①∠BAE=30°,②△ABE~△AEF,③AE⊥EF,④△ADF~△ECF.
其中正确的有 .
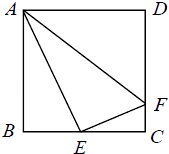 13. 如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB, ,PB=4,则线段AB的长为 .
13. 如图,已知切线PA切圆于点A,割线PBC分别交圆于点B,C,点D在线段BC上,且DC=2BD,∠BAD=∠PAB, ,PB=4,则线段AB的长为 .
三、综合题
-
14. [选修4-1:几何证明选讲]
如图,在正方形ABCD中,E,G分别在边DA,DC上(不与端点重合),且DE=DG,过D点作DF⊥CE,垂足为F.
 (1)、证明:B,C,G,F四点共圆;(2)、若AB=1,E为DA的中点,求四边形BCGF的面积.15. [选修4-1:几何证明选讲]
(1)、证明:B,C,G,F四点共圆;(2)、若AB=1,E为DA的中点,求四边形BCGF的面积.15. [选修4-1:几何证明选讲]如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心, OA为半径作圆.
 (1)、证明:直线A与⊙O相切;(2)、点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.16. 选修4﹣1:几何证明选讲
(1)、证明:直线A与⊙O相切;(2)、点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.16. 选修4﹣1:几何证明选讲如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB并延长交⊙O于点E.证明:
 (1)、AC•BD=AD•AB;(2)、AC=AE.17. 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.
(1)、AC•BD=AD•AB;(2)、AC=AE.17. 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.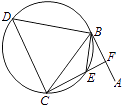 (1)、证明:DB=DC;(2)、设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.18. 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B、E、F、C四点共圆.
(1)、证明:DB=DC;(2)、设圆的半径为1,BC= ,延长CE交AB于点F,求△BCF外接圆的半径.18. 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B、E、F、C四点共圆. (1)、证明:CA是△ABC外接圆的直径;(2)、若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.
(1)、证明:CA是△ABC外接圆的直径;(2)、若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.