2016-2017学年江苏省无锡市宜兴市七年级上学期期末数学试卷

试卷更新日期：2017-03-14 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各数中，比﹣2小的数是（）

A、﹣3 B、﹣1 C、0 D、2

查看试题解析
2. 下列计算正确的是（）

A、3a﹣2b=ab B、5y﹣3y=2 C、7a+a=7a² D、3x²y﹣2yx²=x²y

查看试题解析
3. 已知实数a、b在数轴上对应的点如图所示，则下列式子正确的是（）

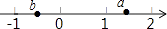A、a•b＞0 B、a+b＜0 C、|a|＜|b| D、a﹣b＞0

查看试题解析
4. 下列关于单项式﹣ $\frac{x y^{3}}{2}$ 的说法中，正确的是（）

A、系数是﹣ $\frac{1}{2}$ ，次数是4 B、系数是﹣ $\frac{1}{2}$ ，次数是3 C、系数是﹣2，次数是4 D、系数是﹣2，次数是3

查看试题解析
5. 如图，C、D是线段AB上两点，若BC=3cm，BD=5cm，且D是AC的中点，则AC的长为（）

A、2cm B、4cm C、8cm D、13cm

查看试题解析
6. 如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD=150°，则∠BOC等于（）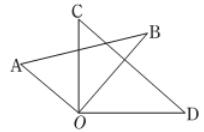

A、30° B、45° C、50° D、60°

查看试题解析
7. 由若干边长相等的小正方体构成的几何体的主视图、左视图、俯视图如图所示，则构成这个几何体的小正方体有（）个．

A、5 B、6 C、7 D、8

查看试题解析
8. 某品牌自行车1月份销售量为100辆，每辆车售价相同，2月份的销售量比1月份增加10%，每辆车的售价比1月份降低了80元，2月份与1月份的销售总额相同，则1月份的售价为（）

A、720元 B、800元 C、880元 D、1080元

查看试题解析
9. 有m辆校车及n个学生，若每辆校车乘坐40名学生，则还有10名学生不能上车；若每辆校车乘坐43名学生，则只有1名学生不能上车．现有下列四个方程：①40m+10=43m﹣1；② $\frac{n + 10}{40}$ = $\frac{n + 1}{43}$ ；③ $\frac{n - 10}{40}$ = $\frac{n - 1}{43}$ ；④40m+10=43m+1．其中正确的是（）

A、①② B、②④ C、②③ D、③④

查看试题解析
10.
将一些半径相同的小圆按如图的规律摆放，第1个图形有4个小圆，第2个图形有8个小圆，第3个图形有14个小圆，…，依次规律，第8个图形的小圆个数是（）

A、58 B、66 C、74 D、80

查看试题解析

二、细心填一填

11. ﹣2017的相反数是．

查看试题解析
12. 据报道，2016年我市城镇非私营单位就业人员平均工资超过70500元，将数70500用科学记数法表示为．

查看试题解析
13. 已知2x^m^﹣¹y⁴与﹣x⁴y²ⁿ是同类项，则mn= ．

查看试题解析
14. 已知∠α=35°28′，则∠α的余角为．

查看试题解析
15. 如图，点A，O，B在一条直线上，且∠AOC=50°，OD平分∠AOC，则∠BOD=度．

查看试题解析
16. 若x=﹣2是关于x的方程2x+m﹣2=0的解，则m的值为．

查看试题解析
17. 如图是一个简单的数值运算程序，当输入n的值为3时，则输出的结果为．

查看试题解析
18. 甲乙二人在环形跑道上同时同地出发，同向运动．若甲的速度是乙的速度的2倍，则甲运动2周，甲、乙第一次相遇；若甲的速度是乙的速度3倍，则甲运动 $\frac{3}{2}$ 周，甲、乙第一次相遇；若甲的速度是乙的速度4倍，则甲运动 $\frac{4}{3}$ 周，甲、乙第一次相遇，…，以此探究正常走时的时钟，时针和分针从0点（12点）同时出发，分针旋转周，时针和分针第一次相遇．

查看试题解析

三、解答题

19. 计算：

(1)、26﹣17+（﹣6）﹣33

(2)、﹣1⁴﹣ $\frac{1}{6}$ ×[3﹣（﹣3）²]

(3)、先化简，再求值：2ab²﹣3a²b﹣2（a²b+ab²），其中a=1，b=﹣2．

查看试题解析
20. 解方程：

(1)、3（x+1）=9；

(2)、 $\frac{2 x - 1}{3}$ =1﹣ $\frac{2 x - 1}{6}$ ．

查看试题解析
21. 如图，所有小正方形的边长都为1，A，B，C都在格点上．

(1)、过点C画直线AB的平行线（仅利用所给方格纸和直尺作图，下同）；

(2)、过点A画直线BC的垂线，并注明垂足为G；过点A画直线AB的垂线，交BC于点H．

(3)、线段的长度是点A到直线BC的距离；线段AH的长度是点H到直线的距离．

(4)、线段AG、AH的大小关系为：AGAH．理由：．

查看试题解析
22. 如图，C为线段AB的中点，D在线段CB上，且DA=8，DB=6．求：

(1)、AC的长；

(2)、CD的长．

查看试题解析
23. 如图，直线AB、CD相交于点O，OE平分∠BOD，∠AOC=76°，∠DOF=90°，求∠EOF的度数．

查看试题解析
24. 某商场以每件120元的价格购进了某种品牌的衬衫600件，并以每件140元的价格销售了500件，由于天气原因，商场准备采取促销措施，问剩下的衬衫促销价格定为每件多少元时，销售完这批衬衫恰好盈利10800元？

查看试题解析
25. 如下图。

(1)、如图1，若CO⊥AB，垂足为O，OE、OF分别平分∠AOC与∠BOC．求∠EOF的度数；

(2)、如图2，若∠AOC=∠BOD=80°，OE、OF分别平分∠AOD与∠BOC．求∠EOF的度数；

(3)、若∠AOC=∠BOD=α，将∠BOD绕点O旋转，使得射线OC与射线OD的夹角为β，OE、OF分别平分∠AOD与∠BOC．若α+β≤180°，α＞β，则∠EOC= ．（用含α与β的代数式表示）

查看试题解析
26. 如图，已知数轴上点A表示的数为8，B是数轴上位于点A左侧一点，且AB=20，动点P从A点出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＜0）秒．

(1)、写出数轴上点B表示的数；点P表示的数（用含t的代数式表示）

(2)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向右匀速运动，若点P，Q同时出发，问多少秒时P，Q之间的距离恰好等于2？

(3)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速到家动，若点P，Q同时出发，问多少秒时P，Q之间的距离恰好又等于2？

(4)、若M为AP的中点，N为BP的中点，在点P运动的过程中，线段MN的长度是否发生变化？若变化，请说明理由，若不变，请他画出图形，并求出线段MN的长．

查看试题解析