2016-2017学年江苏省无锡市锡山区七年级上学期期末数学试卷

试卷更新日期：2017-03-14 类型：期末考试

进入出卷网下载

一、选择题

1. ﹣6的相反数是（）

A、6 B、﹣6 C、 $\frac{1}{6}$ D、- $\frac{1}{6}$

查看试题解析
2. 计算2a²b﹣3a²b的正确结果是（）

A、ab² B、﹣ab² C、a²b D、﹣a²b

查看试题解析
3. 单项式2a²b的系数和次数分别是（）

A、2，2 B、2，3 C、3，2 D、4，2

查看试题解析
4. 已知x=2是方程2x﹣5=x+m的解，则m的值是（）

A、1 B、﹣1 C、3 D、﹣3

查看试题解析
5. 下列去括号正确的是（）

A、a+（b﹣c）=a+b+c B、a﹣（b﹣c）=a﹣b﹣c C、a﹣（b﹣c）=a﹣b+c D、a+（b﹣c）=a﹣b+c

查看试题解析
6. 下列叙述，其中不正确的是（）

A、两点确定一条直线 B、同角（或等角）的余角相等 C、过一点有且只有一条直线与已知直线平行 D、两点之间的所有连线中，线段最短

查看试题解析
7. 射线OC在∠AOB的内部，下列给出的条件中不能得出OC是∠AOB的平分线的是（）

A、∠AOC=∠BOC B、∠AOC+∠BOC=∠AOB C、∠AOB=2∠AOC D、∠BOC= $\frac{1}{2}$ ∠AOB

查看试题解析
8. 如图，小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况，若由图（1）变到图（2），不改变的是（）

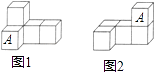A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图

查看试题解析
9. 在同一平面内，已知线段AB的长为10厘米，点A，B到直线l的距离分别为6厘米和4厘米，则符合条件的直线l的条数为（）

A、2条 B、3条 C、4条 D、无数条

查看试题解析
10. 把所有正偶数从小到大排列，并按如下规律分组：（2），（4，6），（8，10，12），（14，16，18，20），…，现有等式A_m=（i，j）表示正偶数m是第i组第j个数（从左往右数）．如A₂=（1，1），A₁₀=（3，2），A₁₈=（4，3），则A₂₀₁₈可表示为（）

A、（45，19） B、（45，20） C、（44，19） D、（44，20）

查看试题解析

二、填空题

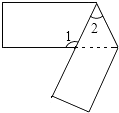
11. ﹣3的倒数是．

查看试题解析
12. 多项式2a³+b²﹣ab³的次数是．

查看试题解析
13. 2017无锡马拉松赛将于2017年3月19日上午7：30发枪，本次比赛设全程马拉松、半程马拉松和迷你马拉松三个项目，其中迷你马拉松需跑3500米，3500用科学记数法表示为．

查看试题解析
14. 在国家房贷政策调控下，某楼盘为促销打算降价销售，原价a元/平方米的楼房，按八五折销售，人们购买该楼房每平方米可节省元．

查看试题解析
15. 已知∠α=34°，则∠α的补角为°．

查看试题解析
16. 用一张长方形纸条折成如图所示图形，如果∠1=130°，那么∠2= ．

查看试题解析
17. 如图，一个长方体的表面展开图中四边形ABCD是正方形，则根据图中数据可得原长方体的体积是 cm³ ．

查看试题解析
18. 小明、小华、小敏三人分别拿出相同数量的钱，合伙订购某种笔记本若干本，笔记本买来后，小明、小华分别比小敏多拿了5本和7本，最后结算时，三人要求按所得笔记本的实际数量付钱，多退少补，结果小明要付给小敏3元，那么，小华应付给小敏元．

查看试题解析

三、解答题

19. 计算：

(1)、（﹣2）²﹣3×（﹣ $\frac{1}{3}$ ）﹣|﹣5|；

(2)、﹣1²⁰¹⁷+0.5÷（﹣ $\frac{1}{2}$ ）³×[2﹣（﹣3）]．

查看试题解析
20. 解方程：

(1)、2（x+8）=3x﹣3；

(2)、 $\frac{x + 1}{2}$ ﹣1=2﹣ $\frac{x - 2}{4}$ ．

查看试题解析
21. 先化简，再求值：3（2a²b﹣ab²）﹣2（﹣ab²+4a²b）+ab² ，其中a=﹣2，b=3．

查看试题解析
22. 如图，已知数轴上A、B两点所表示的数分别为﹣2和8．

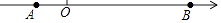(1)、求线段AB的长；

(2)、已知点P为数轴上点A左侧的一点，且M为PA的中点，N为PB的中点．
请你画出图形，观察MN的长度是否发生改变？若不变，求出线段MN的长；若改变，请说明理由．

查看试题解析
23. 如图，直线AB、CD相交于点O，∠BOD=45°，按下列要求画图并回答问题：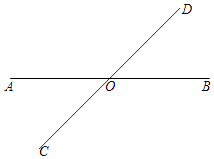

(1)、利用三角尺，在直线AB上方画射线OE，使OE⊥AB；

(2)、利用圆规，分别在射线OA、OE上截取线段OM、ON，使OM=ON，连接MN；

(3)、利用量角器，画∠AOD的平分线OF交MN于点F；

(4)、直接写出∠COF=°．

查看试题解析
24. 如图所示，直线AB、CD相交于点O，OM⊥AB．

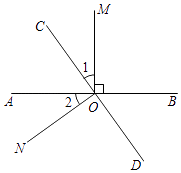(1)、若∠1=∠2，判断ON与CD的位置关系，并说明理由；

(2)、若∠1= $\frac{1}{4}$ ∠BOC，求∠MOD的度数．

查看试题解析

25. 2017年元旦期间，某商场打出促销广告，如表所示．

优惠

条件

一次性购物不超过200元

一次性购物超过200元，但不超过500元

一次性购物超过500元

优惠

办法

没有优惠

全部按九折优惠

其中500元仍按九折优惠，超过500元部分按八折优惠

小欣妈妈两次购物分别用了134元和490元．

(1)、小欣妈妈这两次购物时，所购物品的原价分别为多少？

(2)、若小欣妈妈将两次购买的物品一次全部买清，则她是更节省还是更浪费？说说你的理由．

查看试题解析

26. 已知数轴上有A，B，C三点，分别代表﹣30，﹣10，10，两只电子蚂蚁甲，乙分别从A，C两点同时相向而行，甲的速度为4个单位/秒，乙的速度为6个单位/秒．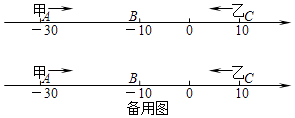

(1)、甲，乙在数轴上的哪个点相遇？

(2)、多少秒后，甲到A，B，C的距离和为48个单位？

(3)、在甲到A，B，C的距离和为48个单位时，若甲调头并保持速度不变，则甲，乙还能在数轴上相遇吗？若能，求出相遇点；若不能，请说明理由．

查看试题解析