2015-2016学年四川省成都市成华区七年级下学期期中数学试卷
试卷更新日期:2017-03-14 类型:期中考试
一、选择题
-
1. 如果一个角是50°,那么它的余角的度数是( )A、40° B、50° C、100° D、130°2. 下列运算中,正确的是( )A、x3+x3=2x6 B、x2•x3=x6 C、x18÷x3=x6 D、(x2)3=x63. 将0.00000573用科学记数法表示为( )A、0.573×10﹣5 B、5.73×10﹣5 C、5.73×10﹣6 D、0.573×10﹣64. 下列各式中,能用平方差公式进行计算的是( )A、(﹣x﹣y)(x+y) B、(2x﹣y)(y﹣2x) C、(1﹣ x)(﹣1﹣ x) D、(3x+y)(x﹣3y)5. 如图,下列能判定AB∥CD的条件有( )个
①∠1=∠2 ②∠3=∠4
③∠B=∠5 ④∠B+∠BCD=180°.
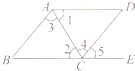 A、1 B、2 C、3 D、46. 若关于x的二次三项式x2﹣ax+36是一个完全平方式,那么a的值是( )A、12 B、±12 C、6 D、±67. 如图,已知直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3=( )
A、1 B、2 C、3 D、46. 若关于x的二次三项式x2﹣ax+36是一个完全平方式,那么a的值是( )A、12 B、±12 C、6 D、±67. 如图,已知直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3=( )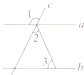 A、40° B、50° C、60° D、70°8. 若(x﹣3)(x+5)=x2+ax+b,则a+b的值是( )A、﹣13 B、13 C、2 D、﹣159. 一个圆柱的底面半径为Rcm,高为8cm,若它的高不变,将底面半径增加了2cm,体积相应增加了192πcm,则R=( )A、4cm B、5cm C、6cm D、7cm10. 某星期天小李步行取图书馆看书,途中遇到一个红灯,停下来耽误了几分钟,为了赶时间,他以更快速度步行到图书馆,下面几幅图是步行路程s(米)与行进时间t(分)的关系的示意图,你认为正确的是( )A、
A、40° B、50° C、60° D、70°8. 若(x﹣3)(x+5)=x2+ax+b,则a+b的值是( )A、﹣13 B、13 C、2 D、﹣159. 一个圆柱的底面半径为Rcm,高为8cm,若它的高不变,将底面半径增加了2cm,体积相应增加了192πcm,则R=( )A、4cm B、5cm C、6cm D、7cm10. 某星期天小李步行取图书馆看书,途中遇到一个红灯,停下来耽误了几分钟,为了赶时间,他以更快速度步行到图书馆,下面几幅图是步行路程s(米)与行进时间t(分)的关系的示意图,你认为正确的是( )A、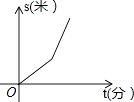 B、
B、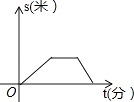 C、
C、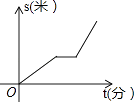 D、
D、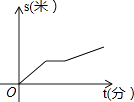
二、填空题
-
11. 若长方形的面积是3a2+2ab+3a,长为3a,则它的宽为 .12. 若5m=3,5n=2,则52m+n= .13. 计算:( )2015×(﹣ )2016=14. 如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是 , 因变量是 .
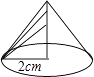 15. 已知x+y=5,xy=2,则(x+2)(y+2)= .
15. 已知x+y=5,xy=2,则(x+2)(y+2)= .三、解答题
-
16. 解答题。(1)、计算:(﹣1)2015+( )﹣3﹣(π﹣3.1)0(2)、计算:(﹣2x2y)2•3xy÷(﹣6x2y)(3)、先化简,再求值:[(2x+y)2+(2x+y)(y﹣2x)﹣6y]÷2y,其中x=﹣ ,y=3.(4)、用整式乘法公式计算: .17. 已知:|3﹣xy|+(x+y﹣2)2=0,求x2+y2+4xy的值.18. 阅读下列推理过程,在括号中填写理由.
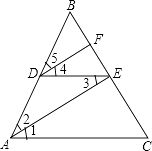
已知:如图,点D,E分别在线段AB、BC上,AC∥DE,DF∥AE交BC于点F,AE平分∠BAC.求证:DF平分∠BDE
证明:∵AE平分∠BAC(已知)
∴∠1=∠2()
∵AC∥DE(已知)
∴∠1=∠3()
故∠2=∠3()
∵DF∥AE(已知)
∴∠2=∠5()
∴∠3=∠4()
∴DE平分∠BDE()
 19. 图中反映了某地某一天24h气温的变化情况,请仔细观察分析图象,回答下列问题:
19. 图中反映了某地某一天24h气温的变化情况,请仔细观察分析图象,回答下列问题: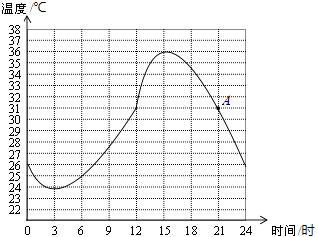 (1)、上午9时的温度是多少?(2)、这一天的最高温度是多少?几时达到最高温度?(3)、这一天的温差是多少?在什么时间范围内温度在下降?(4)、A点表示什么?几时的温度与A点表示的温度相同?20. 如图,点D,F在线段AB上,点E,G分别在线段BC和AC上,CD∥EF,∠1=∠2.
(1)、上午9时的温度是多少?(2)、这一天的最高温度是多少?几时达到最高温度?(3)、这一天的温差是多少?在什么时间范围内温度在下降?(4)、A点表示什么?几时的温度与A点表示的温度相同?20. 如图,点D,F在线段AB上,点E,G分别在线段BC和AC上,CD∥EF,∠1=∠2.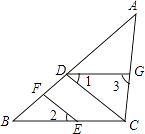 (1)、判断DG与BC的位置关系,并说明理由;(2)、若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,试说明AB与CD有怎样的位置关系?21. 若多项式5x2+2x﹣2与多项式ax+1的乘积中,不含x2项,则常数a= .22. 若∠1与∠2互补,∠3与30°互余,∠2+∠3=210°,则∠1=度.23. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1= , ∠2= .
(1)、判断DG与BC的位置关系,并说明理由;(2)、若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,试说明AB与CD有怎样的位置关系?21. 若多项式5x2+2x﹣2与多项式ax+1的乘积中,不含x2项,则常数a= .22. 若∠1与∠2互补,∠3与30°互余,∠2+∠3=210°,则∠1=度.23. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D,C分别在M,N的位置上,若∠EFG=56°,则∠1= , ∠2= .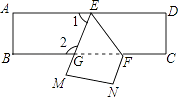 24. 已知(a﹣4)(a﹣2)=3,则(a﹣4)2+(a﹣2)2的值为25. 若规定符号 的意义是: =ad﹣bc,则当m2﹣2m﹣3=0时, 的值为 .26. 如下图:
24. 已知(a﹣4)(a﹣2)=3,则(a﹣4)2+(a﹣2)2的值为25. 若规定符号 的意义是: =ad﹣bc,则当m2﹣2m﹣3=0时, 的值为 .26. 如下图: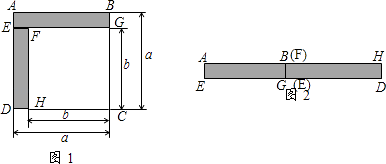 (1)、如图1,已知正方形ABCD的边长为a,正方形FGCH的边长为b,长方形ABGE和EFHD为阴影部分,则阴影部分的面积是(写成平方差的形式)(2)、将图1中的长方形ABGE和EFHD剪下来,拼成图2所示的长方形,则长方形AHDE的面积是(写成多项式相乘的形式)(3)、比较图1与图2的阴影部分的面积,可得乘法公式 .(4)、利用所得公式计算:2(1+ )(1+ )(1+ )(1+ )+ .27. 已知动点P以2cm/s的速度沿图1所示的边框从B→C→D→E→F→A的路径运动,记△ABP的面积为t(cm2),y与运动时间t(s)的关系如图2所示.
(1)、如图1,已知正方形ABCD的边长为a,正方形FGCH的边长为b,长方形ABGE和EFHD为阴影部分,则阴影部分的面积是(写成平方差的形式)(2)、将图1中的长方形ABGE和EFHD剪下来,拼成图2所示的长方形,则长方形AHDE的面积是(写成多项式相乘的形式)(3)、比较图1与图2的阴影部分的面积,可得乘法公式 .(4)、利用所得公式计算:2(1+ )(1+ )(1+ )(1+ )+ .27. 已知动点P以2cm/s的速度沿图1所示的边框从B→C→D→E→F→A的路径运动,记△ABP的面积为t(cm2),y与运动时间t(s)的关系如图2所示.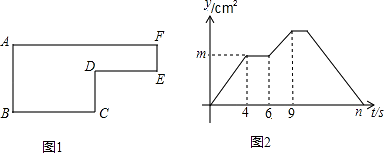
若AB=6cm,请回答下列问题:
(1)、求图1中BC、CD的长及边框所围成图形的面积;(2)、求图2中m、n的值.28. 如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M,N分别在l1、l2上,点M,N,P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.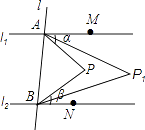 (1)、当点P在l1与l2之间时.
(1)、当点P在l1与l2之间时.求∠APB的大小(用含α、β的代数式表示);
(2)、若∠APM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)(3)、当点P不在l1与l2之间时.若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)