浙江省杭州市余杭区2016-2017学年八年级上学期数学期中考试试卷

试卷更新日期：2018-10-26 类型：期中考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段能组成三角形的是（）

A、1，2，3 B、1， $\sqrt{2}$ ，3 C、3，4，8 D、4，5，6

查看试题解析
2. 能把一个三角形分成面积相等的两部分的是该三角形的（）

A、角平分线 B、中线 C、高 D、一边的垂直平分线

查看试题解析
3. 能说明命题“对于任何实数a，|a|＞﹣a”是假命题的一个反例可以是（）

A、a=﹣2 B、a= $\frac{1}{3}$ C、a=1 D、a= $\sqrt{2}$

查看试题解析
4. 在 $Δ A B C$ 中， $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$ ，则 $∠ C$ 等于（）．

A、 $75^{\circ}$ B、 $60^{\circ}$ C、 $45^{\circ}$ D、 $90^{\circ}$

查看试题解析
5. 如图，已知 $∠ A B C = ∠ B A D$ ，添加下列条件还不能判定 $Δ A B C$ ≌ $Δ B A D$ 的是（）

A、 $A C = B D$ B、 $∠ C A B = ∠ D B A$ C、 $∠ C = ∠ D$ D、 $B C = A D$

查看试题解析
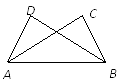6. 等腰三角形的腰长为 $10$ ，底长为 $12$ ，则其底边上的中线长为（）．

A、 $64$ B、 $25$ C、 $13$ D、 $8$

查看试题解析
7. 下列命题中：（1）形状相同的两个三角形全等；（2）斜边和一条直角边对应相等的两个直角三角形一定全等；（3）等腰三角形两腰上的高线相等；（4）三角形的三条高线交于三角形内一点．其中真命题的个数有（）．

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 如图，△ABC为等边三角形，D，E分别是AC，BC上的点，且AD=CE，AE与BD相交于点P，BF⊥AE于点F．若BP=4，则PF的长（）

A、2 B、3 C、1 D、8

查看试题解析
9. 如图， $R t Δ A B C$ 中， $A B = 9$ ， $B C = 6$ ， $∠ B = 90^{\circ}$ ，将 $Δ A B C$ 折叠，使 $A$ 点与 $B C$ 的中点 $D$ 重合，折痕为 $P Q$ ，则线段 $B Q$ 的长度为（）．

A、 $\frac{5}{3}$ B、 $4$ C、 $\frac{5}{2}$ D、 $5$

查看试题解析
10. 在 $Δ A B C$ 中， $∠ A B C = 30^{\circ}$ ， $A B$ 边长为 $4$ ， $A C$ 边的长度可以在 $1$ 、 $2$ 、 $3$ 、 $4$ 、 $5$ 中取值，满足这些条件的互不全等的三角形的个数是（）．

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

11. 命题“两直线平行，同位角相等．”的逆命题是．

查看试题解析
12. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 36^{\circ}$ ， $B D$ 平分 $∠ A B C$ ，则 $∠ 1$ 的度数是．

查看试题解析
13. 已知一个直角三角形的两边长分别为3和4，则第三边长是

查看试题解析
14. 如图，在等腰直角 $Δ A B C$ 中， $∠ C = 90^{\circ}$ ，点 $O$ 是 $A B$ 的中点，且，将一块直角三角板的直角顶点放在点 $O$ 处，始终保持该直角三角板的两直角边分别与 $A C$ 、 $B C$ 相交，交点分别为 $D$ 、 $E$ ，则 $C D + C E =$ ．

查看试题解析
15. 如图，在 $Δ A B C$ 中， $∠ A B C$ 和 $∠ A C B$ 的平分线相交于点 $O$ ，过点 $O$ 作 $E F / / B C$ 交 $A B$ 于 $E$ ，交 $A C$ 于 $F$ ，过点 $O$ 作 $O D ⊥ A C$ 于 $D$ ，下列四个结论：
① $E F = B E + C F$ ；② $∠ B O C = 90^{\circ} + \frac{1}{2} ∠ A$ ；③点 $O$ 到 $Δ A B C$ 各边的距离相等；④设 $O D = m$ ， $A E + A F = n$ ，则 $S_{Δ A E F} = m n$ ．其中正确的结论是． (填序号)

查看试题解析

三、解答题

16. 如图，在正方形 $A B C D$ 中， $A B = 2$ ，延长 $B C$ 到点 $E$ ，使 $C E = 1$ ，连接 $D E$ ，动点 $P$ 从点 $A$ 出发以每秒 $1$ 个单位的速度沿 $A B \to B C \to C D \to D A$ 向终点 $A$ 运动，设点 $P$ 的运动时间为 $t$ 秒，当 $Δ A B P$ 和 $Δ D C E$ 全等时， $t$ 的值为．

查看试题解析
17. 如图，在 $∠ D C E$ 内部找一个点 $P$ ，使点 $P$ 到 $A$ 、 $B$ 两点的距离相等且到 $∠ D C E$ 两边的距离也相等，请做出点 $P$ （尺规作图，不要求写做法，保留作图痕迹）．

查看试题解析
18. 已知：如图，在 $Δ A B C$ 中， $A B = A C$ ， $D$ 为 $C A$ 延长线上一点， $D E ⊥ B C$ ，交线段 $A B$ 于点 $F$ ．请找出一组相等的线段（ $A B = A C$ 除外）并加以证明．

查看试题解析
19. 如图，在 $Δ A B C$ 中， $∠ C = 90^{\circ}$ ， $B E$ 平分 $∠ A B C$ ， $A F$ 平分外角 $∠ B A D$ ， $B E$ 与 $F A$ 交于点 $E$ ，求 $∠ E$ 的度数．

查看试题解析
20. 如图，点 $E$ 在 $Δ A B C$ 的外部，点 $D$ 边 $B C$ 上， $D E$ 交 $A C$ 于点 $F$ ，若 $∠ 1 = ∠ 2$ ， $A E = A C$ ， $B C = D E$ ．

(1)、求证： $A B = A D$ ；

(2)、若 $∠ 1 = 60^{\circ}$ ，判断 $Δ A B D$ 的形状，并说明理由．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A B = A D = 8$ ， $∠ A = 60^{\circ}$ ， $B C = 10$ ， $C D = 6$ ．
求：

(1)、 $∠ A D C$ 的度数；

(2)、四边形 $A B C D$ 的面积．

查看试题解析
22. 如图，在 $Δ A B C$ 中， $A D$ 是 $B C$ 边上的高线， $C E$ 是 $A B$ 边上的中线， $D G ⊥ C E$ 于 $G$ ， $C D = A E$ ．

(1)、写出 $C G$ 与 $E G$ 的数量关系，并说明理由．

(2)、若 $B D = 8$ ， $C D = 5$ ，求：①点 $E$ 到线段 $B C$ 的距离；② $C E$ 的长(结果保留根号)．

查看试题解析
23. 如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．

(1)、若固定三根木条 $A B$ ， $B C$ ， $A D$ 不动， $A B = A D = 2 c m$ ， $B C = 5 c m$ ，如图，量得第四根木条 $C D = 5 c m$ ，判断此时 $∠ B$ 与 $∠ D$ 是否相等，并说明理由．

(2)、若固定二根木条 $A B$ ， $B C$ 不动， $A B = 2 c m$ ， $B C = 5 c m$ ，量得木条 $C D = 5 c m$ ， $∠ B = 90^{\circ}$ ，写出木条 $A D$ 的长度可能取到的一个值（直接写出一个即可）．

(3)、若固定一根木条 $A B$ 不动， $A B = 2 c m$ ，量得木条 $C D = 5 c m$ ．如果木条 $A D$ ， $B C$ 的长度不变，当点 $D$ 移到 $B A$ 的延长线上时，点 $C$ 也在 $B A$ 的延长线上；当点 $C$ 移到 $A B$ 的延长线上时，点 $A$ ， $C$ ， $D$ 能构成周长为 $30 c m$ 的三角形，求出木条 $A D$ ， $B C$ 的长度．

查看试题解析