人教版八年级数学上册第一次月考a卷
试卷更新日期:2018-10-26 类型:月考试卷
一、选择题
-
1. 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是( )
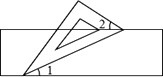 A、15° B、25° C、35° D、45°2. 下列四个图形中,线段BE是△ABC的高的是( )
A、15° B、25° C、35° D、45°2. 下列四个图形中,线段BE是△ABC的高的是( )
A、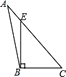 B、
B、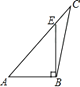 C、
C、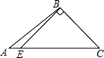 D、
D、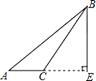 3. 在△ABC和△DEF中,条件:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F;则下列各组给出的条件不能保证△ABC≌△DEF的是( )
3. 在△ABC和△DEF中,条件:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F;则下列各组给出的条件不能保证△ABC≌△DEF的是( )
A、①②③ B、①②⑤ C、 ②⑤⑥ D、①③⑤4. 如图,在△ABC中,AB=AC,AB的中垂线DE交AC于点D,交AB于点E,如果BC=10,△DBC的周长为22,那么AB=( )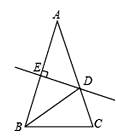
A、10 B、12 C、14 D、165. 如图,在△ABC中,AD是角平分线,AE是高,已知∠B=40°,∠C=60°,那么∠DAE为( )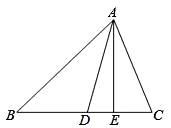 A、10 ° B、15° C、20° D、25°6. 如图,射线AD,BE,CF构成∠1,∠2,∠3,则∠1+∠2+∠3=( )
A、10 ° B、15° C、20° D、25°6. 如图,射线AD,BE,CF构成∠1,∠2,∠3,则∠1+∠2+∠3=( )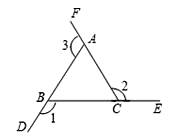 A、180° B、360° C、540° D、无法确定7. 如图,AD是△ ABC中∠ BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2, AB=4,则AC长是( )
A、180° B、360° C、540° D、无法确定7. 如图,AD是△ ABC中∠ BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2, AB=4,则AC长是( )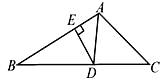 A、3 B、4 C、6 D、58. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.
A、3 B、4 C、6 D、58. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等. A、1 B、1或3 C、1或7 D、3或79. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( )
A、1 B、1或3 C、1或7 D、3或79. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( ) A、19.2° B、8° C、6° D、3°
A、19.2° B、8° C、6° D、3°二、填空题
-
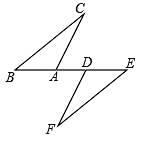
10. 将命题“对顶角相等”改写成“如果…那么…”的形式: .11. 如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是 . (只填一个即可)
 12. 如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 .
12. 如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是 .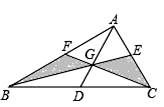 13. 用直尺和圆规作一个角等于已知角的示意图如图,则要说明 ,需要 证明△ ≌△DOC,则这两个三角形全等的依据是(写出全等的简写)
13. 用直尺和圆规作一个角等于已知角的示意图如图,则要说明 ,需要 证明△ ≌△DOC,则这两个三角形全等的依据是(写出全等的简写)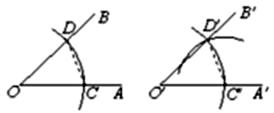 14. 如图,等边ΔABC的边长为1cm,D、E分别是AB、AC上的点,将ΔABC沿直线DE折叠,点A落在A′处,且A′在ΔABC外部,则阴影部分图象的周长为cm.
14. 如图,等边ΔABC的边长为1cm,D、E分别是AB、AC上的点,将ΔABC沿直线DE折叠,点A落在A′处,且A′在ΔABC外部,则阴影部分图象的周长为cm.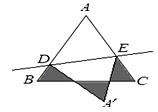 15. 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 s.
15. 如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 s.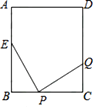
三、解答题
-
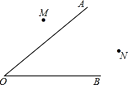
16. 请你直尺和圆规作图(要求:不必写作法,但要保留作图时留下的作图痕迹)
已知:∠AOB,点M、N.求作:点P,使点P到OA、OB的距离相等,且PM=PN.
 17. 若一个三角形的两边分别为2和7,而第三边长为奇数,求此三角形的周长.18. 把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:①∠C=∠F;②AC∥DF.
17. 若一个三角形的两边分别为2和7,而第三边长为奇数,求此三角形的周长.18. 把下面的推理过程补充完整,并在括号内注明理由.如图,点B、D在线段AE上,BC∥EF,AD=BE,BC=EF,试说明:①∠C=∠F;②AC∥DF.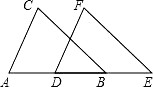
解:∵AD=BE(已知)
∴AD+DB=DB+()
即AB=DE
∵BC∥EF(已知)
∴∠ABC=∠()
又∵BC=EF(已知)
∴△ABC≌△DEF()
∴∠C=∠F,∠A=∠FDE()
∴AC∥DF()
19. 如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.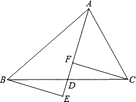 20. 如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
20. 如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.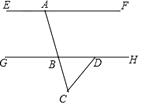 21. 在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
21. 在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.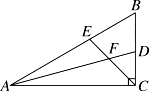 (1)、求∠EFD的度数;(2)、判断FE与FD之间的数量关系,并证明你的结论.
(1)、求∠EFD的度数;(2)、判断FE与FD之间的数量关系,并证明你的结论.
22. CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α。 (1)、若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
(1)、若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE ▲ CF; EF ▲ |BE-AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件,使①中的两个结论仍然成立,并证明两个结论成立;
(2)、如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明)。