浙江杭州拱墅区锦绣育才2017-2018学年七年级上学期数学期中考试试卷
试卷更新日期:2018-10-26 类型:期中考试
一、单选题
-
1. 据某市统计局核算, 年全市实现地区生产总值 亿元,比上年增长 ,经济增速在全国 个省市中居第几位.请将 亿元用科学记数法表示是( ).A、 元 B、 元 C、 元 D、 元2. 若 , , ,则 、 、 的大小关系是( ).A、 B、 C、 D、3. 下列各式运算正确的是( ).A、 B、 C、 D、4. 下列说法正确结论的序号是( ).
( ) 的算术平方根是 ;( ) 平方根是 ;( )当 或 时, ;( ) 的立方根是 .
A、( )( )( )( ) B、( )( ) C、( )( )( ) D、( )5. 已知,当 时, 的值是 ,当 时, 的值是( ).
A、 B、 C、 D、无法确定6. 某商品降价 后欲恢复原价,则提价的百分数为( ).A、 B、 C、 D、7. 在期末复习课上,老师要求写出几个与实数有关的结论:小明同学写了以下 个:①任何无理数都是无限小数;②有理数与数轴上的点一一对应;③在 和 之间的无理数有且只有 、 、 、 这 个;④ 是分数,它是有理数;⑤由四舍五入得到的近似数 表示大于或等于 ,而小于 的数.其中正确的个数是( ).
A、 B、 C、 D、8. 如果 ,那么 的值为( ).A、 B、 C、 D、不确定9. 如果,长方形 中有 个形状、大小相同的小长方形,且 , ,则图中阴影部分的面积为( ).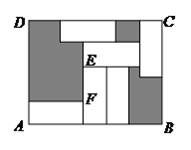 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 观察下列一组数: , , , , , ,根据该组数的排列规律,可推出第 个数是 .11. 已知多项式 的值为 ,则多项式 的值为 .
12. 有理数 , , 在数轴上的位置如图所示,试化简 . 13. 3年前,父亲的年龄是儿子年龄的4倍,3年后父亲的年龄是儿子年龄的3倍,求父子今年各是多少岁?设3年前儿子年龄为x岁,则可列出方程.
13. 3年前,父亲的年龄是儿子年龄的4倍,3年后父亲的年龄是儿子年龄的3倍,求父子今年各是多少岁?设3年前儿子年龄为x岁,则可列出方程.
14. 关于 的方程 解为自然数,当 为整数时,则 的值为 .15. 若关于 的多项式 与 的和是一个单项式,且 ,则 的值为 .
三、解答题
-
16. 计算或解方程
(1)、 .
(2)、(3)、 .(4)、 .17.
(1)、若 、 都是实数,且 ,求 的立方根.
(2)、若 的整数部分为 ,小数部分为 ,求 的值.18.
(1)、已知 与 是同类项, 的系数为 , 的次数是 ,计算 的值.
(2)、求当 , 时,代数式 的值.
19. 小颖解方程 去分母时,方程右边的 没有乘以 ,因而求得方程的解为 ,求 的值,并正确地求出方程的解.20. 已知: , .(1)、若 ,求多项式 .(2)、若 的值与 无关,求 的值.21. 温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地 台,杭州厂可支援外地 台.现在决定给武汉 台,南昌 台.每台机器的运费(单位:百元)如表.设杭州运往南昌的机器为 台.南昌
武汉
温州厂
杭州厂
(1)、用 的代数式来表示总运费(单位:百元).
(2)、若总运费为 元,则杭州运往南昌的机器应为多少台?
(3)、试问有无可能使总运费是 元?若有可能,请写出相应的调运方案;若无可能,请说明理由.22. 东南中学租用两辆小轿车(设速度相同)同时送二名带队老师及 名七年级的学生到育才中学参加数学竞赛,每辆车限坐 人(不包括司机).其中一辆小轿车在距离育才中学 的地方出现故障,此时距离竞赛开始还有 分钟,唯一可利用的交通工具是另一辆小轿车,且这辆车的平均速度是 ,人步行的速度是 (上、下车时间忽略不计).(1)、小李提议:可以让另一辆小轿车先送 名学生走,再返回来接我们.你认为小李的提议合理吗?通过计算说明理由.(2)、小罗提议:可以让另一辆小车先送 名学生走,而其它 名师生同时步行前往,小轿车到达考场后再返回途中接送其他人.你认为小罗的提议合理吗?通过计算说明理由.