2015-2016学年山东省枣庄市滕州市八年级下学期期中数学试卷

试卷更新日期：2017-03-13 类型：期中考试

进入出卷网下载

一、选择题

1. 若x＞y，则下列等式不一定成立的是（）

A、x+4＞y+4 B、﹣3x＜﹣3y C、 $\frac{x}{3} > \frac{y}{3}$ D、x²＞y²

查看试题解析
2. 下列图形中，中心对称图形有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图，在△ABC中，AB=AD=DC，∠B=70°，则∠C的度数为（）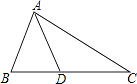

A、35° B、40° C、45° D、50°

查看试题解析
4. 不等式x﹣3≤3x+1的解集在数轴上表示如下，其中正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（）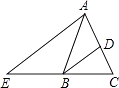

A、40° B、45° C、60° D、70°

查看试题解析
6. 不等式组 ${\begin{matrix} 2 x > - 1 \\ - 3 x + 9 \geq 0 \end{matrix}$ 的所有整数解的和是（）

A、2 B、3 C、5 D、6

查看试题解析
7. 在平面直角坐标系中，把点P（﹣5，3）向右平移8个单位得到点P₁ ，再将点P₁绕原点旋转90°得到点P₂ ，则点P₂的坐标是（）

A、（3，﹣3） B、（﹣3，3） C、（3，3）或（﹣3，﹣3） D、（3，﹣3）或（﹣3，3）

查看试题解析
8. 如果不等式组 ${\begin{matrix} x < 5 \\ x < m \end{matrix}$ 的解集为＜5，那么m的取值范围是（）

A、m＞5 B、m≥5 C、m＜5 D、m≤5

查看试题解析
9. 如图，在△ABC中，AB=AC，AB的垂直平分线DE交AC于D，交AB于E，∠DBC=15°，则∠A的度数是（）

A、50° B、20° C、30° D、25°

查看试题解析
10. 如图，将一个含有45°角的直角三角板的直角顶点放在一张宽为2cm的矩形纸带边沿上，另一个顶点在纸带的另一边沿上．若测得三角板的一边与纸带的一边所在的直线成30°角，则三角板最长边的长是（）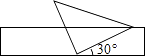

A、2cm B、4cm C、2 $\sqrt{2}$ cm D、4 $\sqrt{2}$ cm

查看试题解析
11. 若a＜﹣1，那么不等式（a+1）x＞a+1的解集为（）

A、x＞1 B、x＜1 C、x＞﹣1 D、x＜﹣1

查看试题解析
12. 如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）

A、35° B、40° C、50° D、65°

查看试题解析
13. 滕州市出租车的收费标准是：起步价6元（即行驶距离不超过3千米都需付6元车费），超过3千米以后，每增加1千米，加收1.5元（不足1千米按1千米计）．某人从甲地到乙地路程是x千米，出租车费为16.5元，那么x的最大值是（）

A、11 B、10 C、9 D、8

查看试题解析
14. 如图，∠MON=30°，点A₁、A₂、A₃…在射线ON上，点B₁、B₂、B₃…在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形，若OA₁=1，则△A₇B₇A₈的边长为（）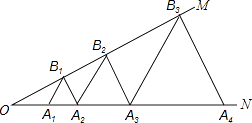

A、6 B、12 C、32 D、64

查看试题解析

二、填空题

15. 若代数式 $\frac{t + 1}{5} - \frac{t - 1}{2}$ 的值不小于1，则t的取值范围是．

查看试题解析
16. 直线l₁：y=x+1与直线l₂：y=mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为．

查看试题解析
17. 在△ABC中，AB=4，AC=3，AD是△ABC的角平分线，则△ABD与△ACD的面积之比是．

查看试题解析
18. 等腰三角形一腰上的高与另一腰的夹角的度数为10°，则顶角的度数为

查看试题解析
19. 若不等式x＜a的正整数解有两个，那么a的取值范围是

查看试题解析
20. 如图，在Rt△ABC中，∠ABC=90°，AB=BC= $\sqrt{2}$ ．将△ABC绕点C逆时针旋转60°，得到△MNC，则AM的长是

查看试题解析

三、解答题

21. 解一元一次不等式（组），并把解集表示在数轴上．

(1)、 $\frac{2 x - 1}{3} \leq x - \frac{x + 1}{2}$

(2)、 ${\begin{matrix} \frac{1}{3} x > \frac{1}{2} x \\ 3 - 5 x \leq 8 \end{matrix}$ ．

查看试题解析
22. 定义新运算：对于任意实数a，b都有：a⊕b=a（a﹣b）+1，如：2⊕5=2×（2﹣5）+1=2×（﹣3）+1=﹣5，求不等式3⊕x＜25的解集．

查看试题解析
23.
△ABC在平面直角坐标系xOy中的位置如图所示，点A的坐标为（﹣2，3），点B的坐标为（﹣1，1），点C的坐标为（0，2）．

(1)、作△ABC关于点C成中心对称的△A₁B_lC_l ．

(2)、将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂ ．

(3)、点P是x轴上的一点，并且使得PA₁+PC₂的值最小，则点P的坐标为（，）．

查看试题解析
24. 如图，已知∠ABC=90°，D是直线AB上的点，AD=BC．过点A作AF⊥AB，并截取AF=BD，连接DC，DF，CF．

(1)、判断△CDF的形状并证明．

(2)、若BC=6，AF=2，求AB的长．

查看试题解析
25. 若方程组 ${\begin{matrix} 2 x + y = k \\ 2 x - y = 1 \end{matrix}$ 的解中，x是正数，y是非正数．

(1)、求k的正整数解；

(2)、在（1）的条件下求一次函数y= $k x - \frac{3}{2}$ 与坐标轴围成的面积．

查看试题解析
26. 如图，在△ABC中，AD是∠BAC的平分线，AD的垂直平分线交BC的延长线于点F．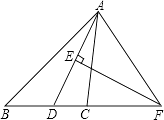

(1)、求证：∠FAD=∠FDA；

(2)、若∠B=50°，求∠CAF的度数．

查看试题解析
27. 某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A、B两种产品共50件．已知生产1件A种产品需甲种原料9千克，乙种原料3千克，可获利700元；生产1件B种产品需甲种原料4千克，乙种原料10千克，可获利1200元．设生产A、B两种产品可获总利润是y元，其中A种产品的生产件数是x．

(1)、写出y与x之间的函数关系式；

(2)、符合题意的生产方案有几种？请你帮忙设计出来；

(3)、如何安排A、B两种产品的生产件数，使总利润y有最大值，并求出y的最大值．

查看试题解析