2015-2016学年江苏省常州市七年级下学期期中数学试卷
试卷更新日期：2017-03-13 类型：期中考试
一、选择题
-
1. 下列各组图形，可由一个图形平移得到另一个图形的是（ ）A、
B、
C、
D、
2. 下列长度的三根木棒首尾相接，能做成三角形框架的是（ ）A、13cm、7cm、5cm B、5cm、7cm、3cm C、7cm、5cm、12cm D、5cm、15cm、9cm3. 下列说法正确的是（ ）A、同位角相等 B、同旁内角相等 C、内错角相等 D、对顶角相等4. 若一个多边形的内角和等于1620°，则这个多边形的边数为（ ）A、9 B、10 C、11 D、125. 多项式x2﹣4x﹣12可以因式分解成（ ）A、x（x﹣4）﹣12 B、（x﹣2）（x+6） C、（x+2）（x﹣6） D、（x+3）（x﹣4）6. 若a3•am=a5÷an ， 则m与n之间的关系是（ ）A、m+n=﹣2 B、m+n=2 C、mn= D、mn=157. 如图，△ABC中，∠BAC=90°，沿AD折叠△ABD，使点B恰好落在AC边上的点E处．若∠C=24°，则∠ADE等于（ ）
A、66° B、69° C、70° D、71°8. 如图，小明从点O出发，沿直线前进10米后向左转n°（0＜n＜90），再沿直线前进10米向左转相同的度数，…照这样走下去，小明发现：当他第一次回到了出发点时，共转过了24次，则小明每次转过的角度n的值为（ ）
A、 B、15 C、 D、36二、填空题
-
9. = ， （﹣2a2b）3= ．10. （﹣0.125）100×8100= ．11. 中国钓鱼岛列岛8个小岛之一的飞濑岛的面积为0.0008平方公里，仅仅只有武进吾悦广场占地面积的 ．用科学记数法表示飞濑岛的面积约为平方公里．12. 一个多边形的每个内角都是144°，则这个多边形的边数为 ．13. 如右图，AB∥CD，直线l分别交AB、CD于E，F，∠1=56°，则∠2的度数是°．
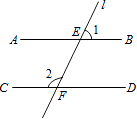14. 若多项式a2﹣12ab+kb2是完全平方式，则常数k的值为 ．15. 若（x+2）（x﹣n）=x2+mx+8，则mn= ．16. 若ma=2，mb=3，mc=4，则m2a+b﹣c= ．17. 如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为 ．
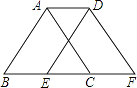18. 在△ABC中，∠B=50°，AD是BC边上的高，且∠DAC=20°，则∠BAC=°．三、解答题
-
19. 计算(1)、﹣12016﹣（π﹣3）0(2)、a5•a4+（﹣2a3）3(3)、2x•（x﹣3y）2(4)、（x﹣y﹣3）（x+y﹣3）20. 因式分解(1)、4x2﹣9y2(2)、3x2y2+12xy+12(3)、a4﹣8a2+16(4)、m2（m﹣n）+n2（n﹣m）21. 已知：a﹣b=2，ab=1，求（a﹣2b）2+3a（a﹣b）的值．22. 如图，在10×10的正方形网格中，每个小正方形的边长为1个单位长度．△ABC的顶点都在正方形网格的格点上，且通过两次平移（沿网格线方向作上下或左右平移）后得到△A′B′C′，点C的对应点是直线上的格点C′．
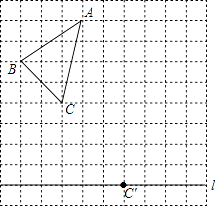(1)、画出△A′B′C′．(2)、△ABC两次共平移了个单位长度．(3)、试在直线上画出点P，使得由点A′、B′、C′、P四点围成的四边形的面积为9．23. 如图，△ABC和△ADC分别在AC的两侧，∠BAC：∠B：∠ACB=4：3：2，且∠DAC=40°．
(1)、试说明AD∥BC．(2)、若AB与CD也平行，求∠D的度数．24. 如图，四边形ABCD中，外角∠DCG=∠A，点E、F分别是边AD、BC上的两点，且EF∥AB．∠D与∠1相等吗？为什么？
25. 小聪是一名非常爱钻研的七年级学生，他将4块完全一样的三角板（如图1）拼成了一个非常工整的图形（如图2），请教老师以后得知：该图形是一个正方形，并且里面的四边形也是一个正方形．为了作进一步的探究，小明将三角板的三边长用为a，b，c表示（如图3），将两个正方形分别用正方形ABCD和正方形EFGH表示，然后他用两种不同的方法计算了正方形ABCD的面积．
(1)、请你用两种不同的方法计算出正方形ABCD面积：方法一：方法二：
(2)、根据（1）中计算结果，你能得到怎么样的结论？(3)、请用文字语言描述（2）中得到的结论．26. 四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交AE于点O，且点O在四边形ABCD的内部．
(1)、如图1，若AD∥BC，∠B=70°，∠C=80°，则∠DOE=°．(2)、如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来