浙江省杭州市西湖区绿城育华2017-2018学年八年级上学期数学期中考试试卷
试卷更新日期:2018-10-26 类型:期中考试
一、单选题
-
1. 给出下面 个式子:① ;② ;③ ;④ ;⑤ ,其中不等式有( ).A、 个 B、 个 C、 个 D、 个2. 下列各组数中,不可能成为一个三角形三边长的是( ).A、 , , B、 , , C、 , , D、 , ,3. 对应命题“若 ,则 ”,下面四组 , 的值中,能说明这个命题是假命题的是( ).
A、 , B、 , C、 , D、 ,4. 如图,直线 ,以直线 上的点 为圆心,适当长为半径画弧,分别交直线 、 于点 、 ,连接 、 .若 ,则 ( ).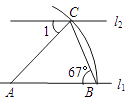 A、 B、 C、 D、5. 如图 ,已知 的六个元素,则图 甲、乙、丙三个三角形中和图 全等的图形是( ).
A、 B、 C、 D、5. 如图 ,已知 的六个元素,则图 甲、乙、丙三个三角形中和图 全等的图形是( ).
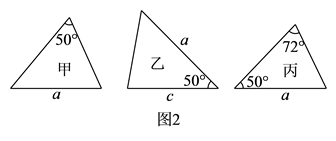 A、甲乙 B、丙 C、乙丙 D、乙6. 已知下列命题:
A、甲乙 B、丙 C、乙丙 D、乙6. 已知下列命题:①若 ,则 ;②若 ,则 ;③有两条边及一个角对应相等的两个三角形全等;④底角相等的两个等腰三角形全等.其中是真命题的个数是( ).
A、 个 B、 个 C、 个 D、 个7. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( ) A、0.7米 B、1.5米 C、2.2米 D、2.4米8. 在 中,点 , 分别在边 , 上,点 , 在边 上,已知 , , , ,则 的度数( ).
A、0.7米 B、1.5米 C、2.2米 D、2.4米8. 在 中,点 , 分别在边 , 上,点 , 在边 上,已知 , , , ,则 的度数( ).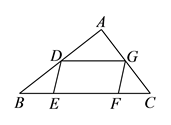 A、等于 B、等于 C、等于 D、条件不足,无法计算9. 如图, 为等边 内一点, , , ,则 的度数为( ).
A、等于 B、等于 C、等于 D、条件不足,无法计算9. 如图, 为等边 内一点, , , ,则 的度数为( ).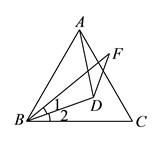 A、 B、 C、 D、10. 如图在 中, , 分别是 、 上的点,作 , ,垂足分别是 , , , ,下面三个结论:① ;② ;③ ≌ .其中正确的是( ).
A、 B、 C、 D、10. 如图在 中, , 分别是 、 上的点,作 , ,垂足分别是 , , , ,下面三个结论:① ;② ;③ ≌ .其中正确的是( ).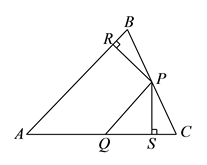 A、①② B、②③ C、①③ D、①②③
A、①② B、②③ C、①③ D、①②③二、填空题
-
11. 请写出一个解集为 的不等式 .12. 命题“相等的角是对顶角”的逆命题是 .13. 如图,在锐角 中, , , 分别是 , 边上的高,且 , 交于点 ,则 度.
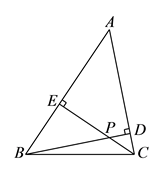 14. 如图,已知 的周长是 , , 分别平分 和 , 于 ,且 , 的面积是 .
14. 如图,已知 的周长是 , , 分别平分 和 , 于 ,且 , 的面积是 .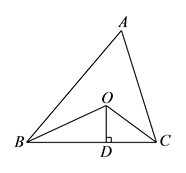 15. 两张完全相同的纸片,每张都分成 个完全相同的矩形,放置如图,重合的顶点记作 ,顶点 在另一张纸的分隔线 上,若 ,则 的长是 .
15. 两张完全相同的纸片,每张都分成 个完全相同的矩形,放置如图,重合的顶点记作 ,顶点 在另一张纸的分隔线 上,若 ,则 的长是 .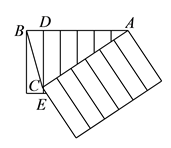 16. 如图,是一张长方形纸片 ,已知 , , 为边 上一点, ,现在要剪下一张等腰三角形纸片( ),要使点 落在长方形 的某一边上,则 的底边长为 .
16. 如图,是一张长方形纸片 ,已知 , , 为边 上一点, ,现在要剪下一张等腰三角形纸片( ),要使点 落在长方形 的某一边上,则 的底边长为 .
三、解答题
-
17. 解不等式 ,并在数轴上表示不等式的解集.18. 如图,在 中, , .
 (1)、尺规作图:作线段 的垂直平分线交 于 ,交 于 .(2)、连结 ,求证: 平分 .19. 如图,正方形网格中的每个小正方形边长都是 ,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)、尺规作图:作线段 的垂直平分线交 于 ,交 于 .(2)、连结 ,求证: 平分 .19. 如图,正方形网格中的每个小正方形边长都是 ,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.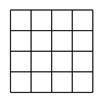

 (1)、画一个三角形,使它的三边长都是有理数.(2)、画一个直角三角形,使它们的三边长都是无理数.(3)、画出与 成轴对称且与 有公共点的格点三角形(画出一个即可).20. 如图, 和 都是等边三角形,点 是 的边 上的一点,连接 , .
(1)、画一个三角形,使它的三边长都是有理数.(2)、画一个直角三角形,使它们的三边长都是无理数.(3)、画出与 成轴对称且与 有公共点的格点三角形(画出一个即可).20. 如图, 和 都是等边三角形,点 是 的边 上的一点,连接 , . (1)、求证: .(2)、求 、 所夹锐角的度数,并写出推理过程.
(1)、求证: .(2)、求 、 所夹锐角的度数,并写出推理过程.
21. 已知 , , 为 上一点, 为 上一点, . (1)、如果 , ,那么 .(2)、如果 , ,那么 , .(3)、设 , 猜想 , 之间的关系式,并说明理由.22. 已知:如图,在 中, ,垂足为点 , ,垂足为点 , 为 边的中点,连结 、 、 .
(1)、如果 , ,那么 .(2)、如果 , ,那么 , .(3)、设 , 猜想 , 之间的关系式,并说明理由.22. 已知:如图,在 中, ,垂足为点 , ,垂足为点 , 为 边的中点,连结 、 、 .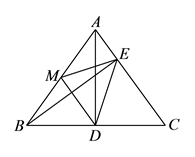 (1)、猜想 的形状,并说明理由.
(1)、猜想 的形状,并说明理由.
(2)、若 , ,求 的面积.23. 问题背景如图 ,在正方形 的内部,作 ,根据三角形全等的条件,易得 ≌ ≌ ≌ ,从而得到四边形 是正方形.
类比探究
如图 ,在正 的内部,作 , , , 两两相交于 , , 三点( , , 三点不重合).

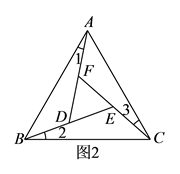
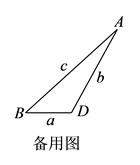 (1)、 , , 是否全等?如果是,请选择其中一对进行证明.(2)、 是否为正三角形?请说明理由.
(1)、 , , 是否全等?如果是,请选择其中一对进行证明.(2)、 是否为正三角形?请说明理由.
(3)、进一步探究发现,图 中的 的三边存在一定的等量关系,设 , , ,请探索 , , 满足的等量关系.