2015-2016学年山东省菏泽市鄄城县八年级下学期期中数学试卷

试卷更新日期：2017-03-13 类型：期中考试

进入出卷网下载

一、选择题

1. 如图，Rt△ABC，∠B=90°，∠C=30°，AC=5cm，则AB的长为（）

A、4cm B、3cm C、2.5cm D、2cm

查看试题解析
2. 已知a＞b，则下列不等式中正确的是（）

A、﹣3a＞﹣3b B、﹣ $\frac{a}{3}$ ＞﹣ $\frac{b}{3}$ C、3﹣a＞3﹣b D、a﹣3＞b﹣3

查看试题解析
3. 如图，将四边形ABCD先向左平移2个单位长度，再向上平移1个单位长度，那么点B的对应点B′的坐标是（）

A、（4，﹣1） B、（﹣4，﹣1） C、（4，1） D、（5，1）

查看试题解析
4. 不等式2x﹣5≤4x﹣3的解集在数轴上表示应为（）

A、 B、 C、 D、

查看试题解析
5. 如图，在△ABC中，AB=AC，AE是经过点A的一条直线，且B，C在AE的两侧，BD⊥AE于D，CE⊥AE于E，AD=CE，则∠BAC的度数是（）

A、45° B、60° C、90° D、120°

查看试题解析
6. 如图，将△ABC绕点A顺时针旋转后，得到△AB′C′，且C′在边BC上，若∠B′C′B′=46°，则∠C的度数为（）

A、56° B、60° C、67° D、70°

查看试题解析
7.
如图是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（　　）

A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条高所在直线的交点 D、△ABC三条角平分线的交点

查看试题解析
8.
如图，在方格纸中，△ABC经过变换得到△DEF，正确的变换是( )

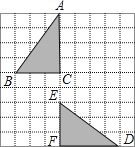A、把△ABC绕点C逆时针方向旋转90°，再向下平移2格　　 B、把△ABC绕点C顺时针方向旋转90°，再向下平移5格　　 C、把△ABC向下平移4格，再绕点C逆时针方向旋转180°　　 D、把△ABC向下平移5格，再绕点C顺时针方向旋转180°

查看试题解析
9. 若关于x的一元一次不等式组 ${\begin{matrix} 1 - 2 x > x - 2 \\ x - a > 0 \end{matrix}$ 无解，则a的取值范围是（）

A、a≥1 B、a＞1 C、a≤﹣1 D、a＜﹣1

查看试题解析
10. 如图，在3×3的网格中，每个网格线的交点称为格点．已知图中A，B两个格点，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的点C有（）

A、4个 B、6个 C、8个 D、10个

查看试题解析

二、填空题

11. 命题“在角的内部，到角的两边距离相等的点在角的平分线上”的逆命题是：．

查看试题解析
12. 如果2x﹣5＜2y﹣5，那么﹣x﹣y（填“＜、＞、或=”）

查看试题解析
13. 如图，图形B是由图形A旋转得到的，则旋转中心的坐标为
．

查看试题解析
14. 某中学举办了“汉字听写大会”，准备为获奖的40名同学颁奖（每人一个书包或一本词典），已知每个书包28元，每本词典20元，学校计划用不超过900元钱购买奖品，则最多可以购买个书包．

查看试题解析
15. 如图，在△ABC中，AB=4，BC=6，∠B=80°，将△ABC沿射线BC的方向平移2个单位后，得到△A′B′C′，连接A′C，则∠B′A′C= ．

查看试题解析
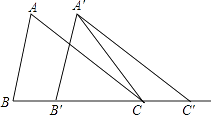16. 如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于D，PE⊥OB于E．若点Q是OC上与O、P不重合的另一点，则以下结论中，一定成立的是（填序号）
①PD=PE；②OC垂直平分DE；③QO平分∠DQE；④△DEQ是等边三角形．

查看试题解析
17. 不等式组 ${\begin{matrix} 3 x \geq 9 ① \\ x < 5 ② \end{matrix}$ 的整数解共有个．

查看试题解析
18. 如图所示，∠AOB=45°，OP平分∠AOB，PC∥OB，PD⊥OB，如果PC=6，那么PD= ．

查看试题解析

三、解答题

19. 解下列不等式（组），并把解集在数轴上表示出来．

(1)、 $\frac{x - 1}{3}$ ≤5﹣x

(2)、 ${\begin{matrix} 3 x + 1 > 4 \\ 4 - 2 x \geq 0 \end{matrix}$ ．

查看试题解析
20. 如图，在Rt△ABC中，∠A=90°，BE平分∠ABC，过点E作BC的垂线交BC于点D，CE=BE．求证：AB=CD．

查看试题解析
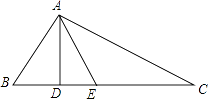
21. 如图，已知△abc的三个顶点的坐标分别为A（﹣6，4），B（﹣4，0），C（﹣2，2）．

(1)、将△ABC向右平移5个单位得，得△A₁B₁C₁ ，画出图形，并直接写出点A₁的坐标；

(2)、将△ABC绕坐标原点O逆时针旋转90°，得△A₂B₂C₂ ，画出图形，并直接写出点B₂的坐标．

查看试题解析
22. 某中学举行了社会主义核心价值教育知识竞赛，试卷共20道题，规定每答对一题记10分，答错或放弃记﹣4分，八年级一班代表队的得分目标为不低于88分，问这个队至少要答对多少道题才能达到目标要求？

查看试题解析
23. 如图，在△ABC中，AD是高，在线段DC上取一点E，使DE=BD，已知AB+BD=DC．
求证：E点在线段AC的垂直平分线上．

查看试题解析
24. 如图，在平面直角坐标系中，点A的坐标为（﹣2，0），等边△AOC经过平移或轴对称或旋转都可以得到△OBD．

(1)、△AOC沿x轴向右平移得到△OBD，则平移的距离是个单位长度；△AOC与△BOD关于直线对称，则对称轴是；△AOC绕原点O顺时针旋转得到△DOB，则旋转角度可以是度．

(2)、连接AD，交OC于点E，求AD的长．

查看试题解析
25. 甲、乙两家超市以相同的价格出售同样的商品．为了吸引顾客，各自推出不同的优惠方案．在甲超市累计购买商品超过300元之后，超出部分按原价八折优惠；在乙超市累计购买商品超出200元之后，超出部分按原价八五折优惠．设顾客累计购物x元（x＞300）．

(1)、若设两家超市购物所付费用分别为y₁ ， y₂ ，请你分别写出y₁ ， y₂与x之间的函数关系式．

(2)、顾客到哪家超市购物更优惠？

查看试题解析
26. 已知△ABC中，∠A=90°，AB=AC，D为BC的中点．

(1)、如图，若E、F分别是AB、AC上的点，且BE=AF．求证：△DEF为等腰直角三角形；

(2)、若E，F分别为AB，CA延长线上的点，仍有BE=AF，其他条件不变，那么△DEF是否仍为等腰直角三角形？证明你的结论．

查看试题解析