2016-2017学年天津市河东区九年级上学期期末数学试卷

试卷更新日期：2017-03-13 类型：期末考试

进入出卷网下载

一、选择题

1. 下列交通标志中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在下列方程中，一元二次方程是（　　）

A、x²﹣2xy+y²=0 B、x（x+3）=x²﹣1 C、x²﹣2x=3 D、x+ $\frac{1}{x}$ =0

查看试题解析
3. 抛物线y=（x﹣2）²+1的顶点坐标是（　　）

A、（﹣2，﹣1） B、（﹣2，1） C、（2，﹣1） D、（2，1）

查看试题解析
4. 从数字2，3，4中任选两个数组成一个两位数，组成的数是偶数的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{5}{6}$

查看试题解析
5. 如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC=（）

A、3cm B、4cm C、5cm D、6cm

查看试题解析
6. 已知正六边形的边长为2，则它的内切圆的半径为（）

A、1 B、 $\sqrt{3}$ C、2 D、2 $\sqrt{3}$

查看试题解析
7. 在反比例函数 $y = \frac{1 - k}{x}$ 的每一条曲线上，y都随着x的增大而减小，则k的值可以是（）

A、﹣1 B、1 C、2 D、3

查看试题解析
8. 用配方法解下列方程时，配方正确的是（）

A、方程x²﹣6x﹣5=0，可化为（x﹣3）²=4 B、方程y²﹣2y﹣2015=0，可化为（y﹣1）²=2015 C、方程a²+8a+9=0，可化为（a+4）²=25 D、方程2x²﹣6x﹣7=0，可化为 ${(x - \frac{3}{2})}^{2} = \frac{23}{4}$

查看试题解析
9. 如图所示，在△ABC中，∠CAB=70°，现将△ABC绕点A顺时针旋转一定角度后得到△AB′C′，连接BB′，若BB′∥AC′，则∠CAB′的度数为（）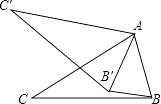

A、20° B、25° C、30° D、40°

查看试题解析
10. 若二次函数y=（x﹣m）²﹣1，当x≤3时，y随x的增大而减小，则m的取值范围是（　　）

A、m=3 B、m＞3 C、m≥3 D、m≤3

查看试题解析
11. 如图，⊙O的半径为4，点P是⊙O外的一点，PO=10，点A是⊙O上的一个动点，连接PA，直线l垂直平分PA，当直线l与⊙O相切时，PA的长度为（）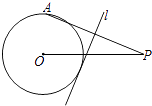

A、10 B、 $\frac{21}{2}$ C、11 D、 $\frac{43}{4}$

查看试题解析
12. 如图是抛物线y=ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间．则下列结论：
①a﹣b+c＞0；
②3a+b=0；
③b²=4a（c﹣n）；
④一元二次方程ax²+bx+c=n﹣1有两个不相等的实数根．
其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题：

13. 方程x²﹣3=0的根是．

查看试题解析
14. 如图，M为反比例函数y= $\frac{k}{x}$ 图象上一点，MA⊥y轴于点A，S_△_MAO=2时，k= ．

查看试题解析
15. 如图，BD是⊙O的直径，∠CBD=30°，则∠A的度数为．

查看试题解析
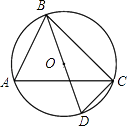16. 若关于x的一元二次方程x²﹣4x+m=0有两个不相等的实数根，则m的取值范围为．

查看试题解析
17. 如图，量角器边缘上有P、Q两点，它们表示的读数分别为60°，30°，已知直径AB=4 $\sqrt{3}$ ，连接PB交OQ于M，则QM的长为．

查看试题解析
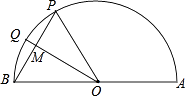18. 如图，在△BDE中，∠BDE=90°，BD=6 $\sqrt{2}$ ，点D的坐标是（7，0），∠BDO=15°，将△BDE旋转到△ABC的位置，点C在BD上，则旋转中心的坐标为．

查看试题解析

三、解答题

19. 解方程：

(1)、3x（x﹣1）=2x﹣2

(2)、x²﹣6x+5=0（配方法）

查看试题解析
20. 如图，转盘A的三个扇形面积相等，分别标有数字1，2，3，转盘B的四个扇形面积相等，分别有数字1，2，3，4．转动A、B转盘各一次，当转盘停止转动时，将指针所落扇形中的两个数字相乘（当指针落在四个扇形的交线上时，重新转动转盘）．

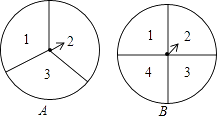(1)、用树状图或列表法列出所有可能出现的结果；

(2)、求两个数字的积为奇数的概率．

查看试题解析
21. 已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．

(1)、如图①，当直线l与⊙O相切于点C时，求证：AC平分∠DAB；

(2)、如图②，当直线l与⊙O相交于点E，F时，求证：∠DAE=∠BAF．

查看试题解析
22. 已知二次函数y=﹣x²+bx+c的图象如图所示，它与x轴的一个交点坐标为（﹣1，0），与y轴的交点坐标为（0，3）．

(1)、求出b、c的值，并写出此二次函数的解析式；

(2)、根据图象，直接写出函数值y为正数时，自变量x的取值范围；

(3)、当2≤x≤4时，求y的最大值．

查看试题解析
23. 如图，某建筑工程队利用一面墙（墙的长度不限），用40米长的篱笆围成一个长方形的仓库．

(1)、求长方形的面积是150平方米，求出长方形两邻边的长；

(2)、能否围成面积220平方米的长方形？请说明理由．

查看试题解析
24. 图1和图2中的正方形ABCD和四边形AEFG都是正方形．

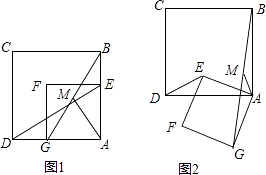(1)、如图1，连接DE，BG，M为线段BG的中点，连接AM，探究AM与DE的数量关系和位置关系，并证明你的结论；

(2)、在图1的基础上，将正方形AEFG绕点A逆时针方向旋转到图2的位置，连结DE、BG，M为线段BG的中点，连结AM，探究AM与DE的数量关系和位置关系，并证明你的结论．

查看试题解析
25.
如图，直线y=﹣ $\frac{1}{2}$ x+1与x轴交于点A，与y轴交于点B，抛物线y=﹣x²+bx+c经过A，B两点．

(1)、求抛物线的解析式；

(2)、点P是第一象限抛物线上的一点，连接PA、PB、PO，若△POA的面积是△POB面积的 $\frac{4}{3}$ 倍．
①求点P的坐标；
②点Q为抛物线对称轴上一点，请直接写出QP+QA的最小值；

(3)、点M为直线AB上的动点，点N为抛物线上的动点，当以点O、B、M、N为顶点的四边形是平行四边形时，请直接写出点M的坐标．

查看试题解析